Lecture 13. Attention

Attention

참조 : https://velog.io/@seoyeon/Lecture-13-Attention

Seq2Seq with RNNs

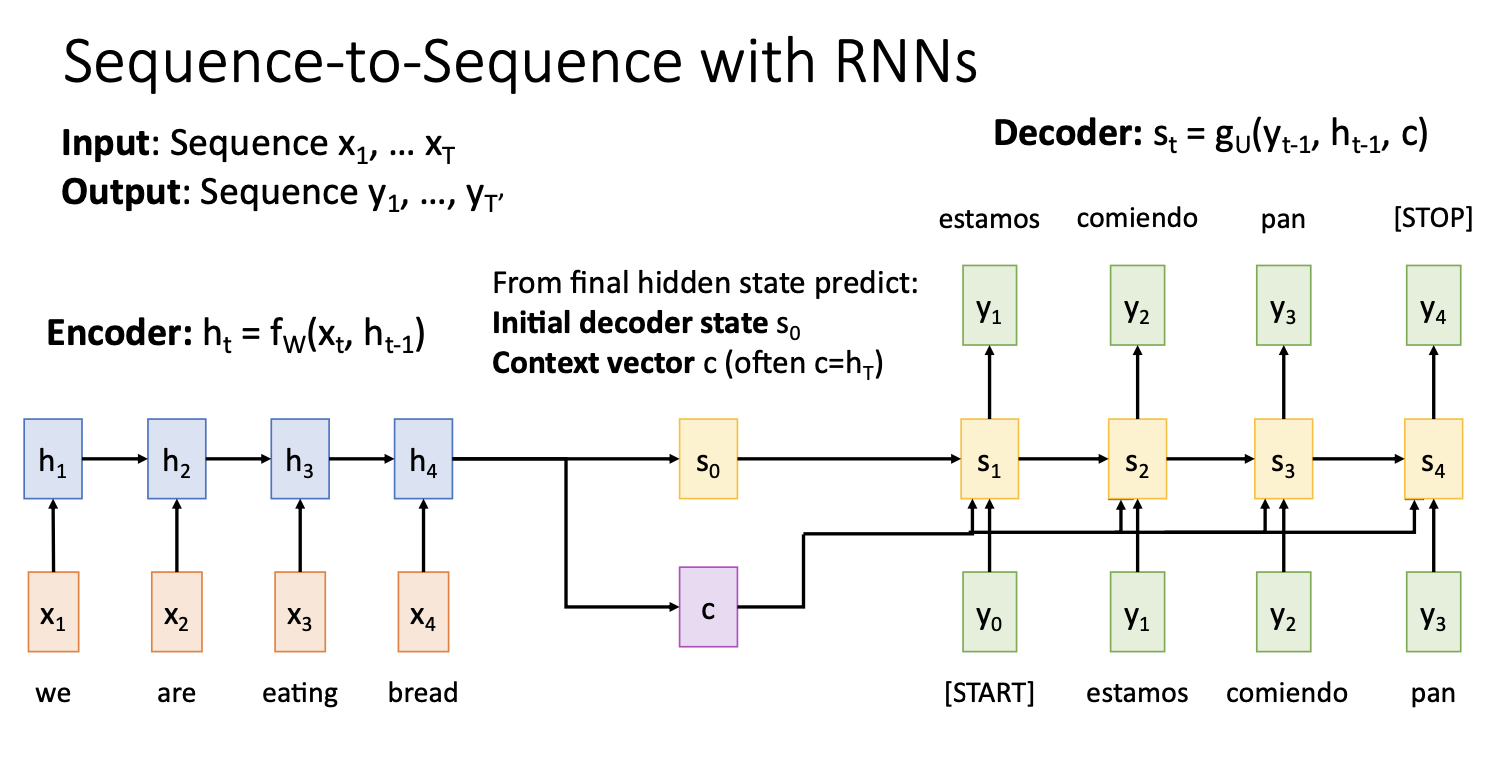
input은 영어문장, output은 스페인어 문장 (영어문장을 스페인어 문장으로 만듦)
encoder에서는 input sequence를 받아서 t만큼의 step을 거쳐 $h_t$ hidden state를 만들고 이것을 decoder의 첫번째 hidden state $s_0$ 와 context vector로 사용함
Decoder에서는 Input인 START token을 시작으로 이전 state(첫번째에서는 $s_0$)와 context vector를 통해서 hidden state $s_t$를 만들고 이를 통해서 output $y_t$를 계산함.
이 Output을 input으로 넣어서 STOP token을 output으로 출력할때까지 step반복
이때 context vector는 Input sequence를 요약하여 decoder의 매 step 에 사용되며 encoded sequence와 decoded sequence사이에서 정보를 전달하는 중요한 역할을 함

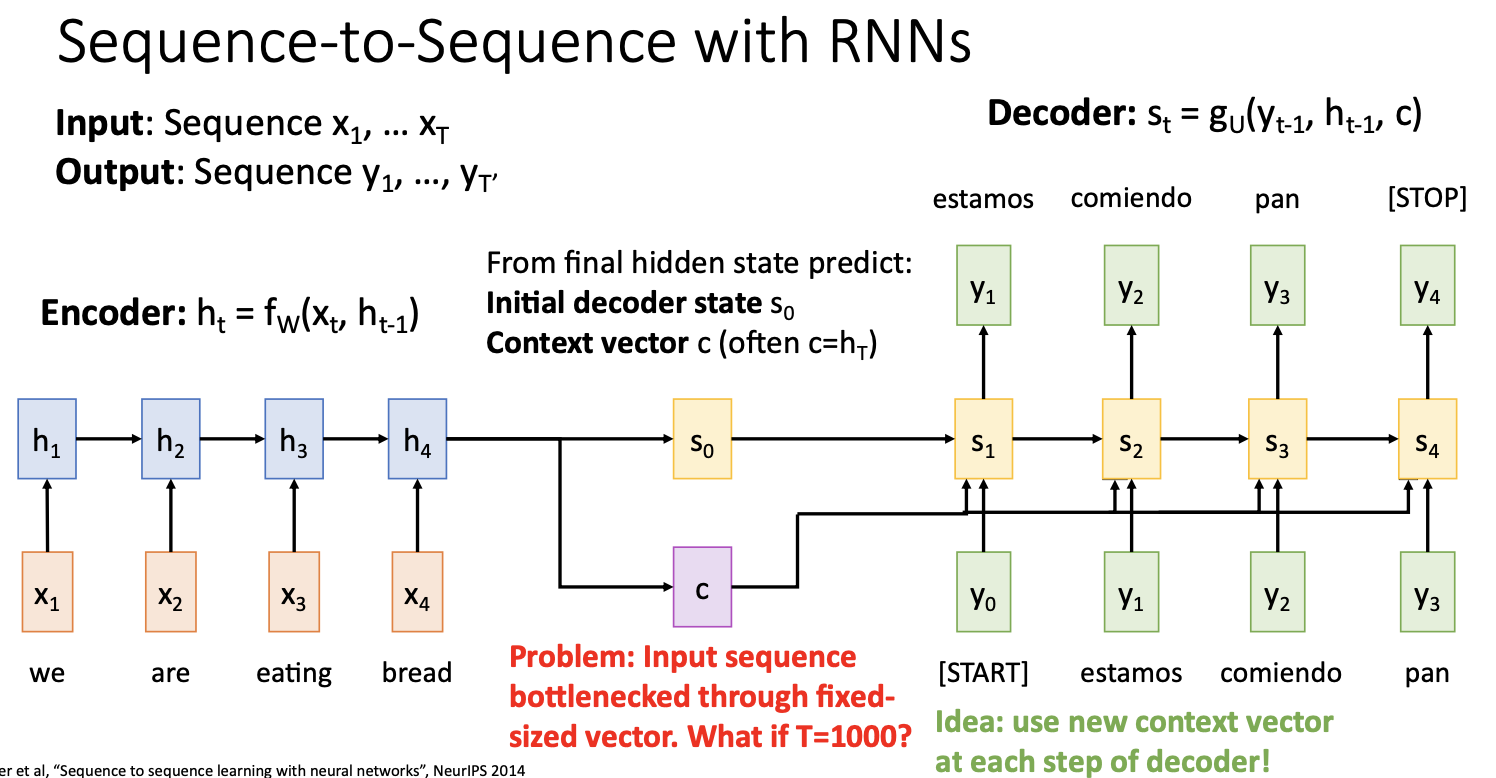
context vector c는 decoder가 sequence를 생성하는데 필요한 모든 입력 문장의 정보를 요약한 것이라서 매우 중요한 역할을 하는데, 매우 긴 문장이나 문서를 처리할 때에는 문제가 있음
하나의 vector로 아주 많은 문장들을 요약하는 과정에서 정보가 bottleneck된다. (input sequence의 정보가 bottleneck되는 것)
이 문제의 해결방안으로 decoder의 매 time step마다 새로운 context vector를 계산하는 것을 생각해 볼 수 있는데 이것이 Attention의 아이디어
자세하게 말하자면, 매 time step마다 decoder가 input sequence의 다른 부분에 초점을 맞춘 새로운 context vector를 선택하도록 하는 것임

Seq2Seq with RNNs and Attention

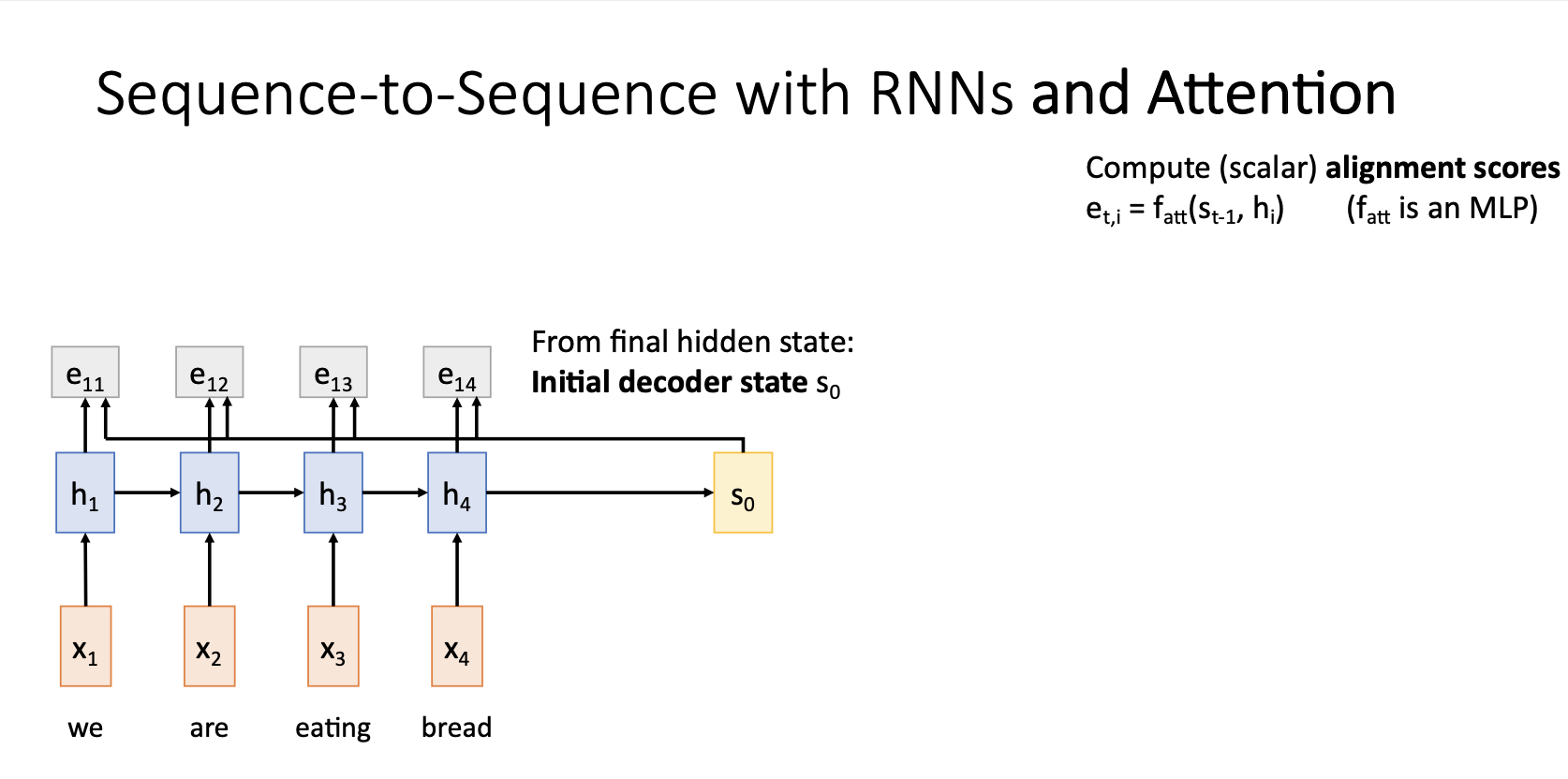
Attention을 적용한 Seq2Seq 모델에서는 alignment function $f_att$ 를 통해서 계산한 alignment score $e_{t,i}$ 를 통해서 decoder의 매 time step마다 새로운 context vector를 생성함
alignment function $f_att$는 decoder의 Hidden state $s_t -1 $ 와 hidden state $h_i$ 를 입력받아 동작하는 아주 작은 fully connected network.

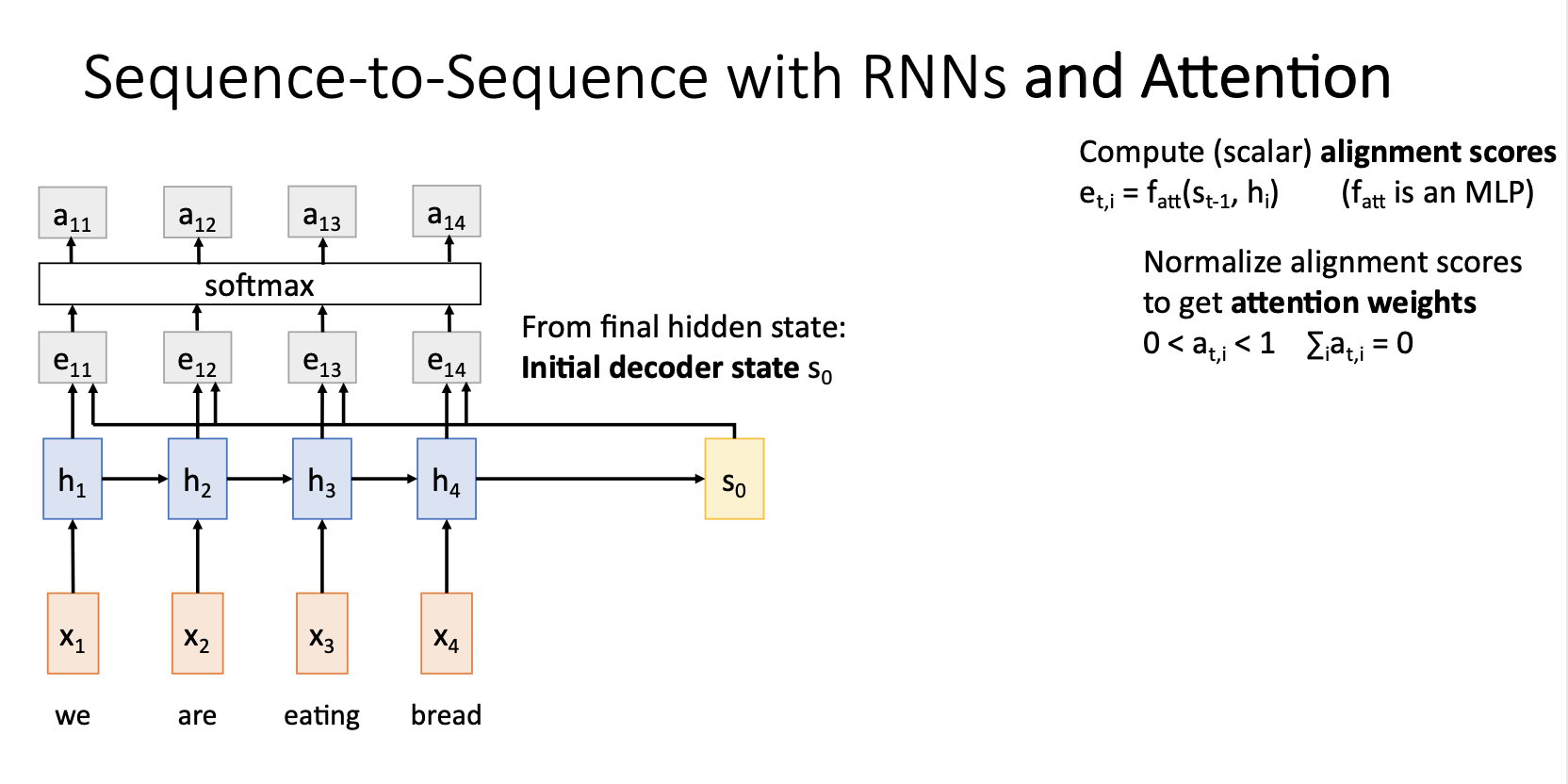
이전의 output score $(e_{t,i})$ 를 softmax를 통해서 0~1 사이의 값을 갖는 probability distribution으로 나타내고 이러한 softmax의 output을 attention weights라고 하고 이는 각 hidden state에 얼마나 가중치를 둘 것이냐를 나타냄

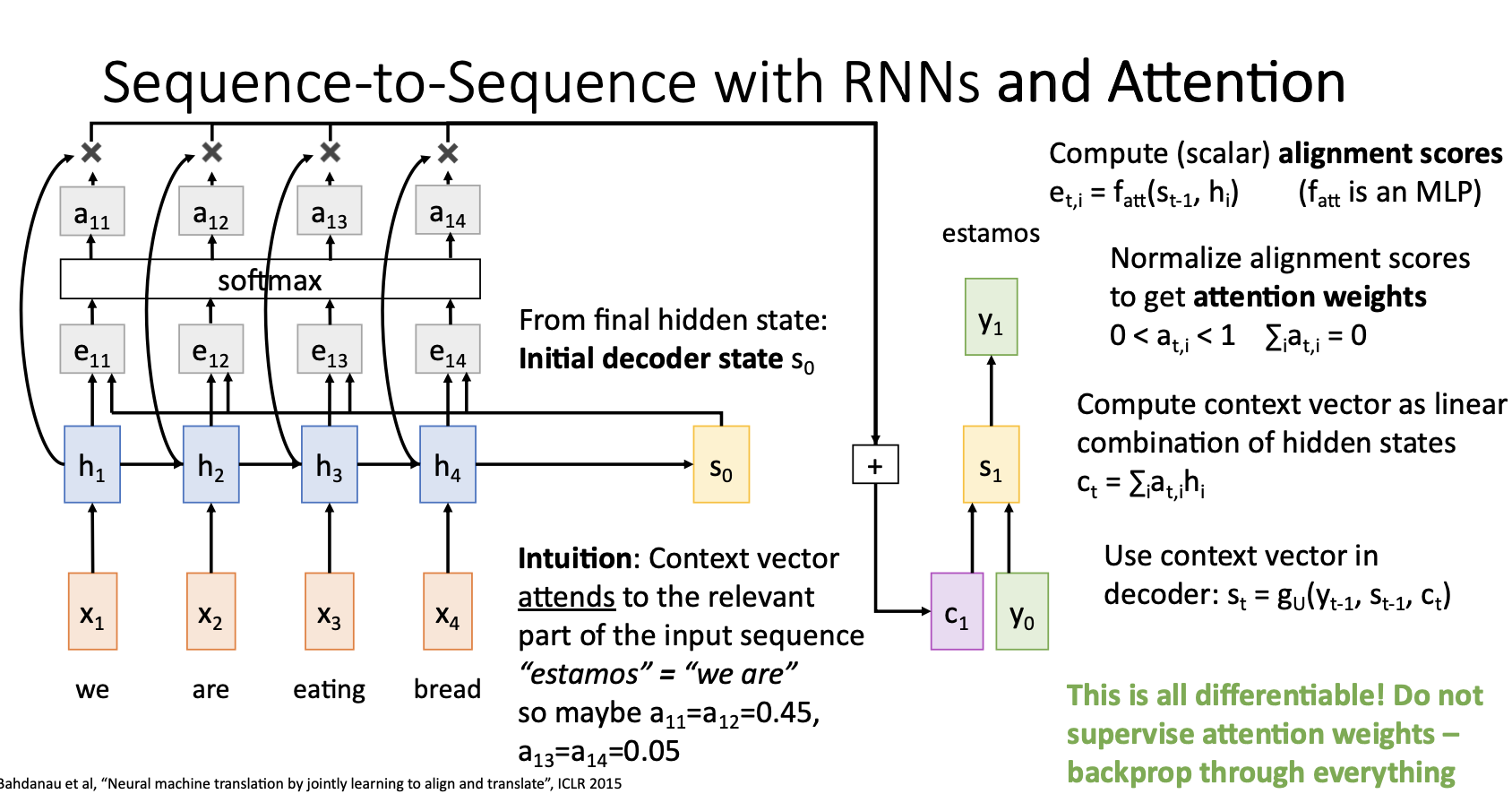
Attention weights와 각 hidden state를 weighted sum 해주어 t시점의 새로운 context vector $c_t$ 를 구해줌
Decoder는 이러한 context vector $c_t$ 와 input $y_t-1$ 이전 state인 $h_t-1$을 사용해서 t 시점의 state $s_t$를 생성하고 이를 통해 predict된 output을 생성해줌
위 그림의 computational graph에 나타나는 모든 연산들은 differntiable하기 때문에 backprop이 가능하고 이로인해 network 가 알아서 decoder의 input의 어느 state에 attention해야하는지 학습하게 됨

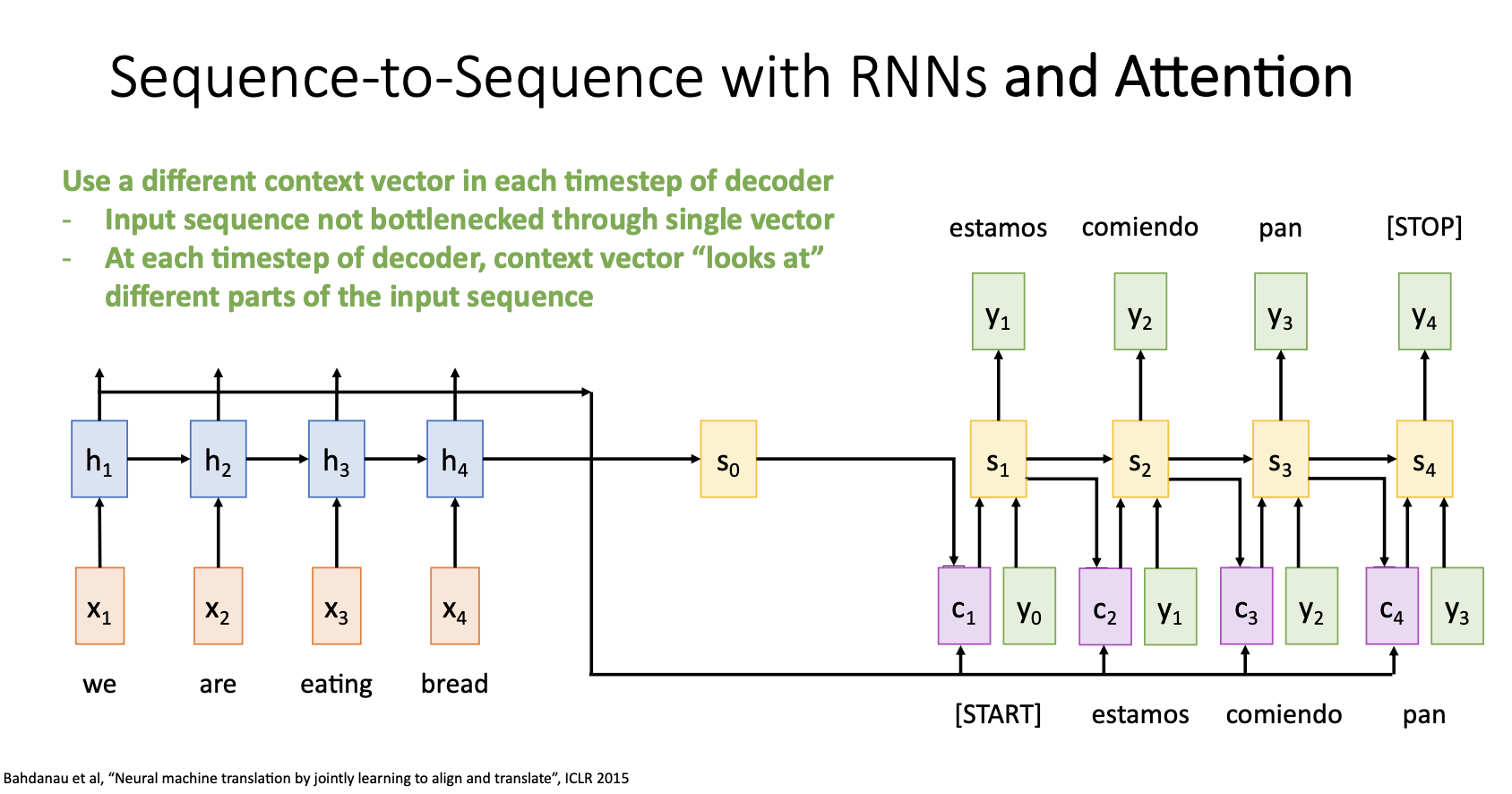
이러한 과정을 decoder의 time step마다 반복해서 사용하고 기존의 seq2seq처럼 decoder가 stop token을 출력하면 멈추게 됨
요약하자면 input sequence의 모든 정보를 하나의 context vector에 요약하는 것 대신에, 디코더의 각 time step마다 새로운 context vector를 생성하도록 유연성을 제공하면서 bottleneck 문제를 해결 . 각 time step의 output마다 input seequence에서 집중할 부분을 스스로 선택하면서 context vector를 생성

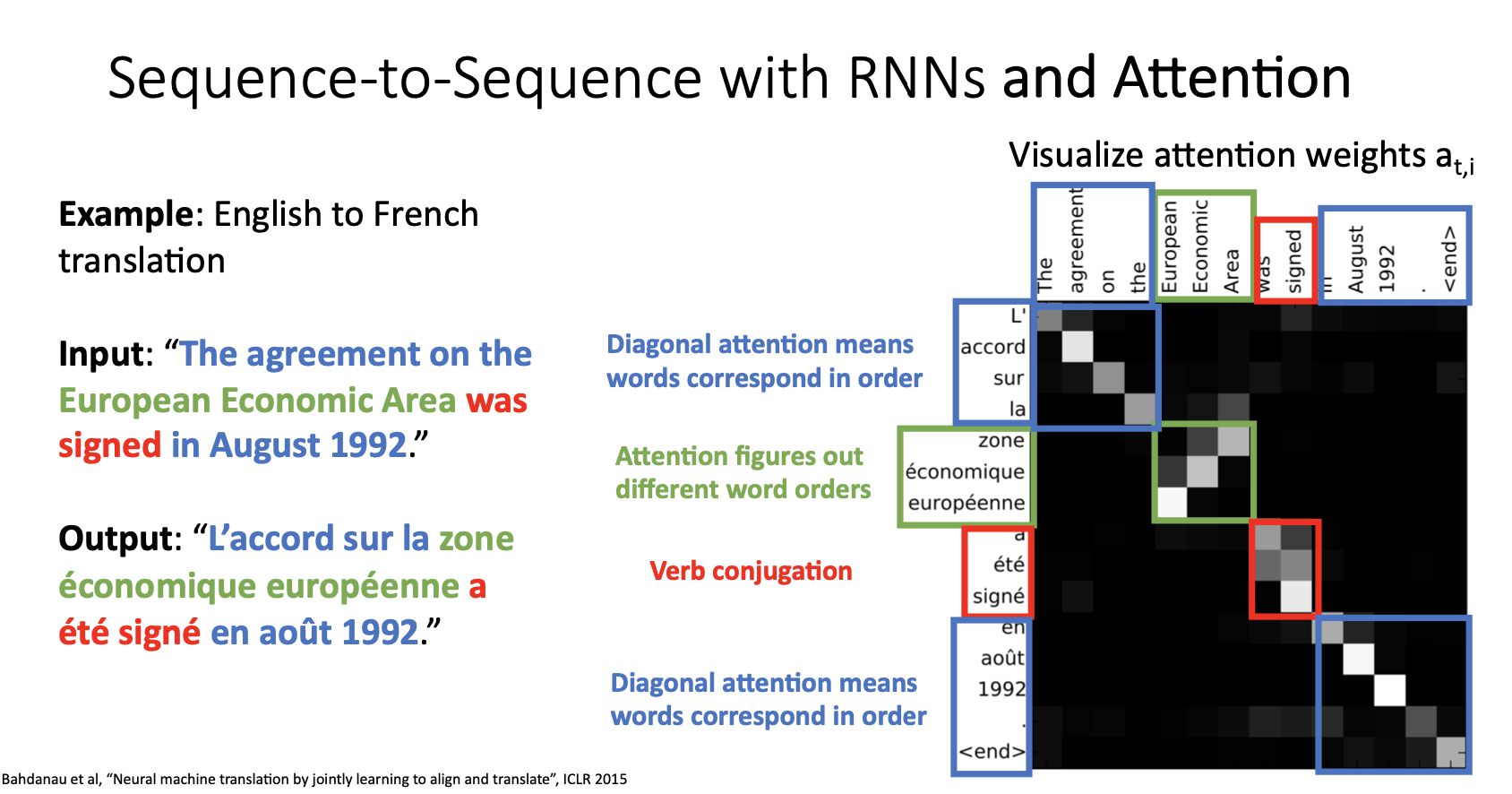
위 그림은 영어를 프랑스어로 번역하는 예시로 seq2seq with attention모델이 decoder 시점별 단어를 생성해낼 때 attention weights를 나타낸 것으로 모델이 시점별로 input의 어느 state에 집중하고 있는지를 보여줌

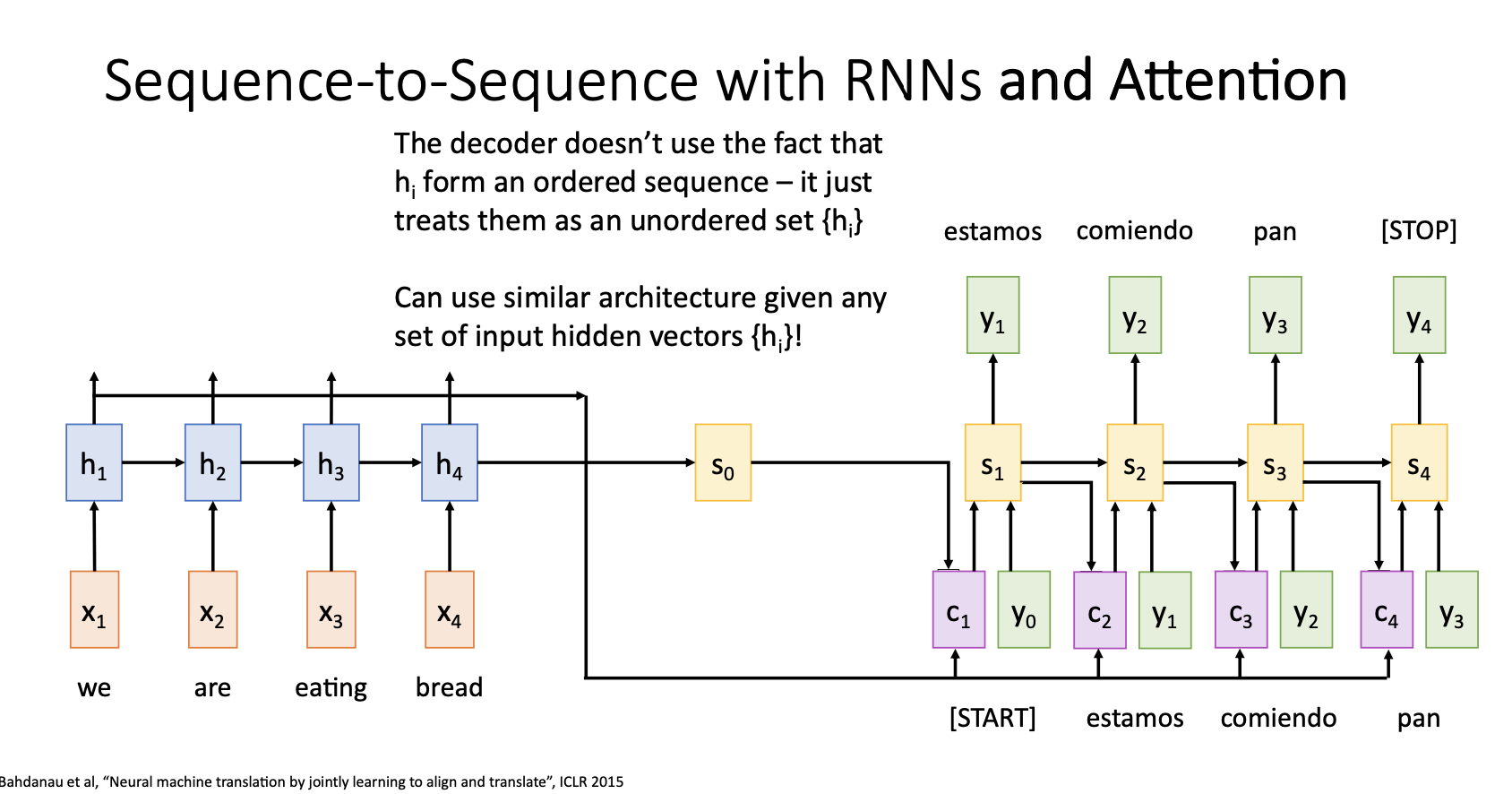
지금까지 기계 번역에 사용한 Attention mechanism의 구조를 자세히 살펴보면, 입력이 시퀀스인지에 대해서 전혀 신경쓰지 않음
이는 입력 데이터의 형태가 시퀀스가 아닌 다른 모델들에도 Attention mechanism을 사용할 수 있다는 것을 의미

Image Captioning with Attention

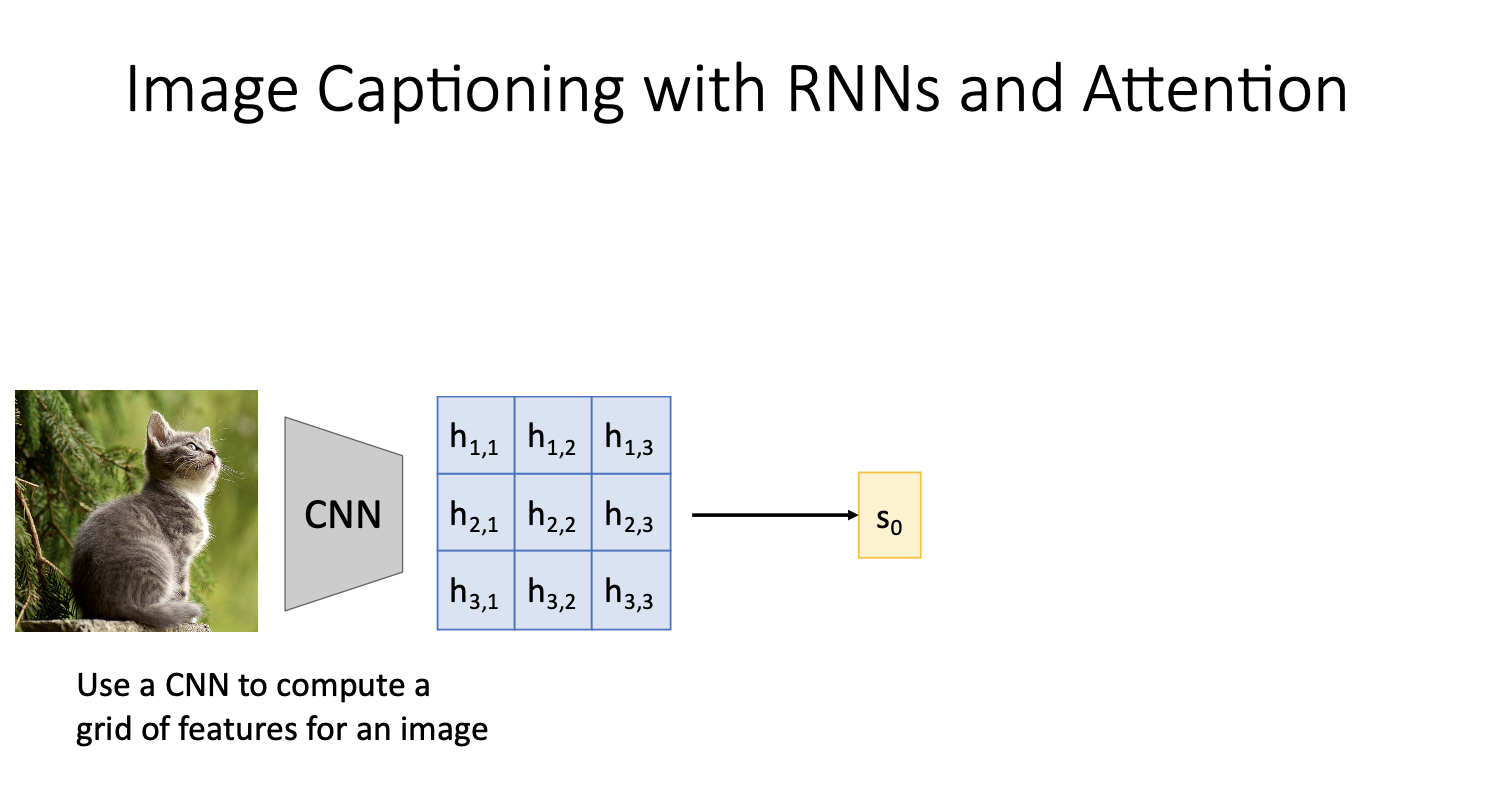
일단 RNN만을 사용한 image captioning에서 FC layer를 통한 feature vector (sequence vector)를 RNN모델의 input으로 사용한 것과 다르게 위 그림처럼 CNN에서 grid of feature vectors를 뽑아내 이것을 RNN모델에 input으로 집어넣는다.
이때 grid of feature veectors는 $(h_{1,1}~h_{3,3})$ 각각 spatial position에 해당됨

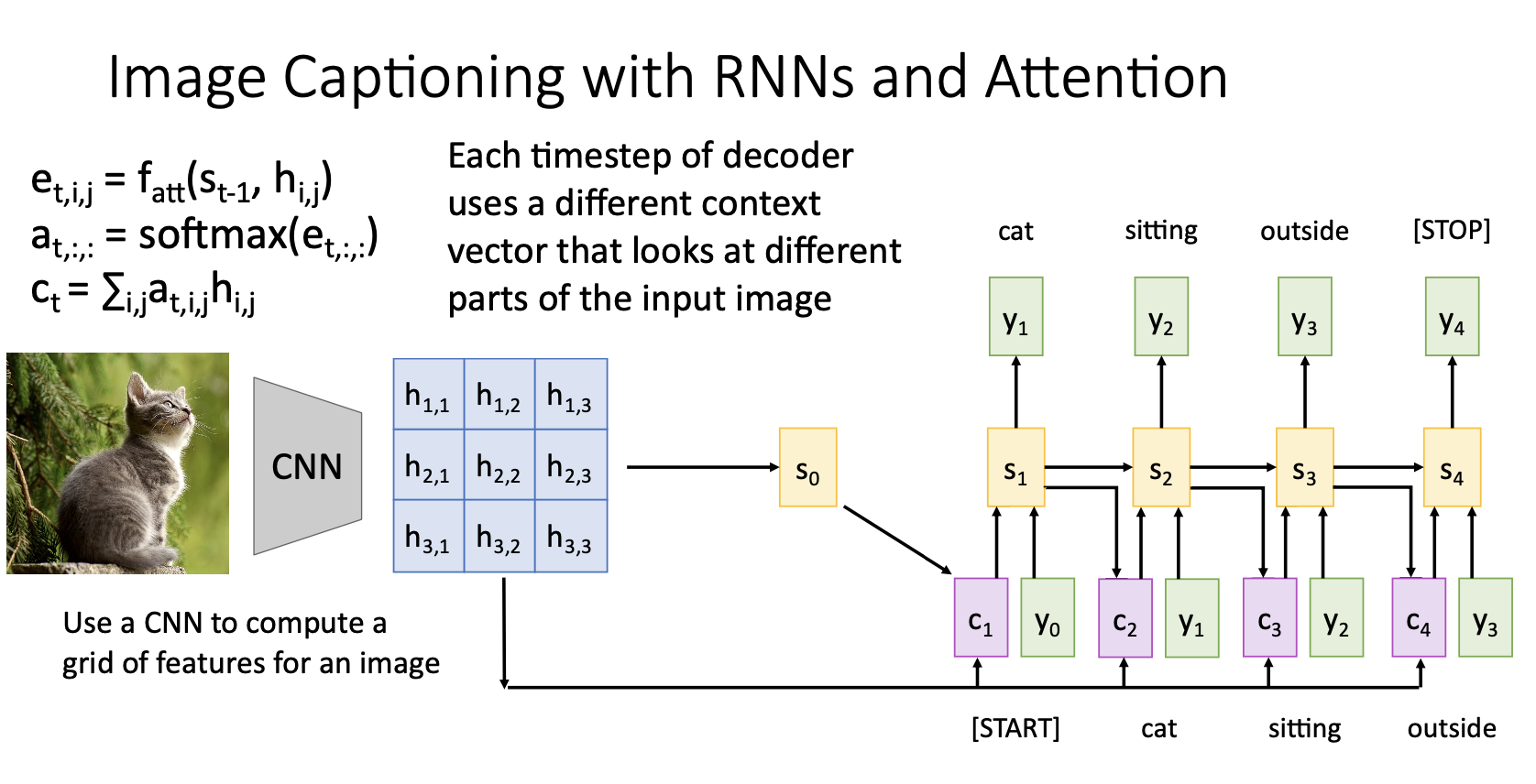
위 과정들을 반복하면 image caption을 모두 생성
Image Captioning에 적용한 attention도 전에 번역문제에서 수행한 것과 매우 유사한 방법
Image Captioning에서의 attention은 결국 image caption의 단어를 생성하는 각 단계에서 grid의 각기 다른 feature vectore들이 decoder의 현재 state인 $s_t$와 weighted sum시켜 새롭게 context vector를 만든 것

Examples

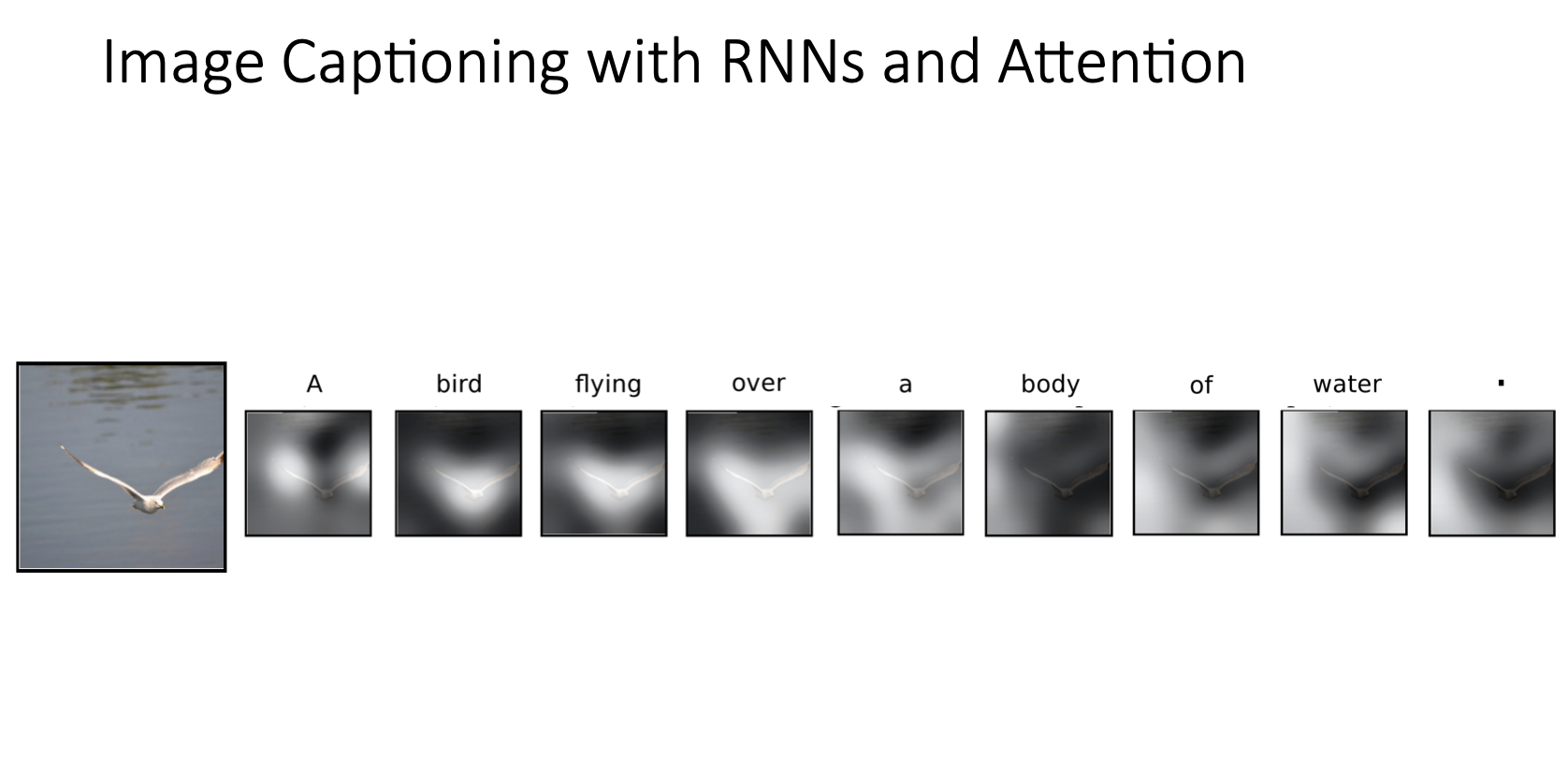
위 그림은 물 위를 날고 있는 새 이미지를 입력으로 받아서 모델이 “A bird flying over a body of water”. 를 출력하는 과정에서 각 문장의 단어별로 image grid에서 높은 가중치를 보이는 부분들을 보여준 것
bird라는 단어부분에서는 새 주변에 하이라이트되어서 높은 가중치를 보였다는 것을 알 수 있음

위 그림은 또 다른 예시인데 밑줄 친 단어들을 생성할 때, 한단어를 생성하는 state에서 입력 이미지의 어떤 곳에 높은 가중치가 부여되어서 attention되는지 시각화 한 것

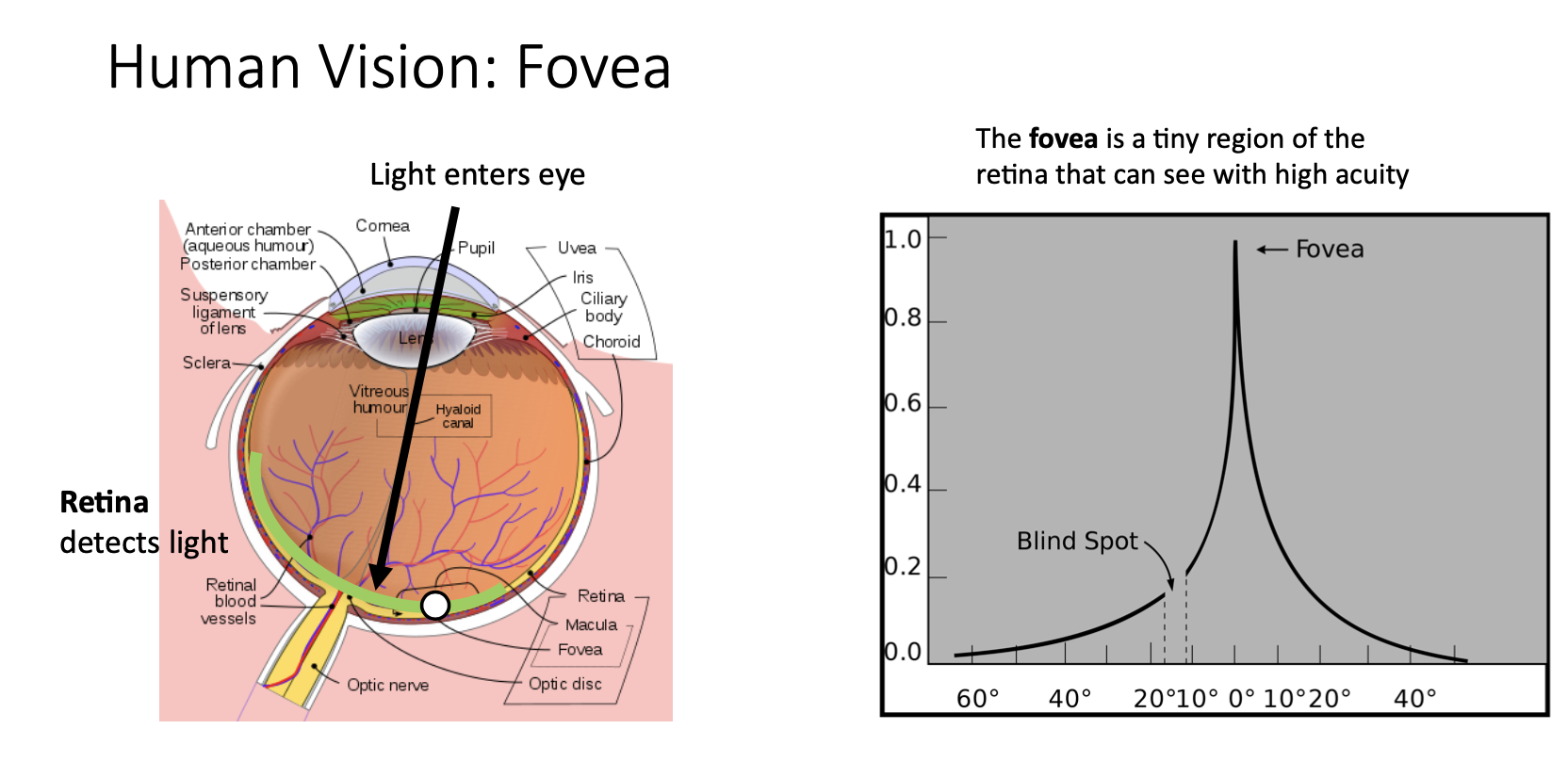
이런 image captioning에서의 attetion은 생물학적인 관점에서 봤을 때 왼쪽 그림을 보면 우리 눈의 망막에는 fovea라는 작은 영역이 있는데 이 곳에 맺히는 상만 선명할 수 있음

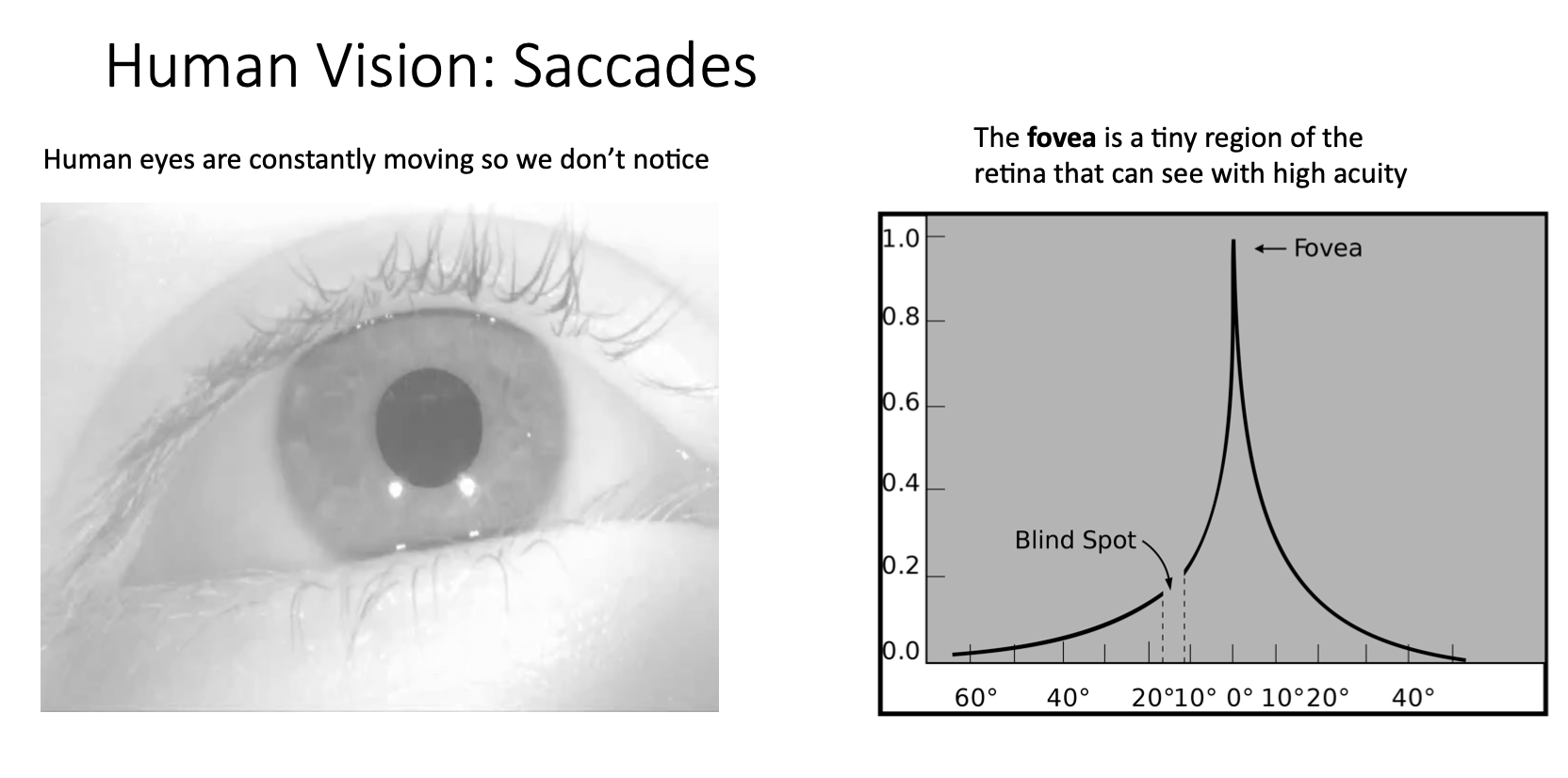
우리가 어떤 풍경을 봤을 때 보이는 풍경들을 한번에 동시에 다 인지하고 있다고 생각할 수 있지만 사실은 그 풍경들을 다 인지하기 위해서 사람의 동공을 바쁘게 움직이면서 인지하고 있는 것
fovea에 맺히는 상만 선명하게 보이는 이런 한계를 극복하기 위해서 사람의 눈이 계속해서 움직이면서 인지하게 되는건데 이런 움직임을 saccade라고 함

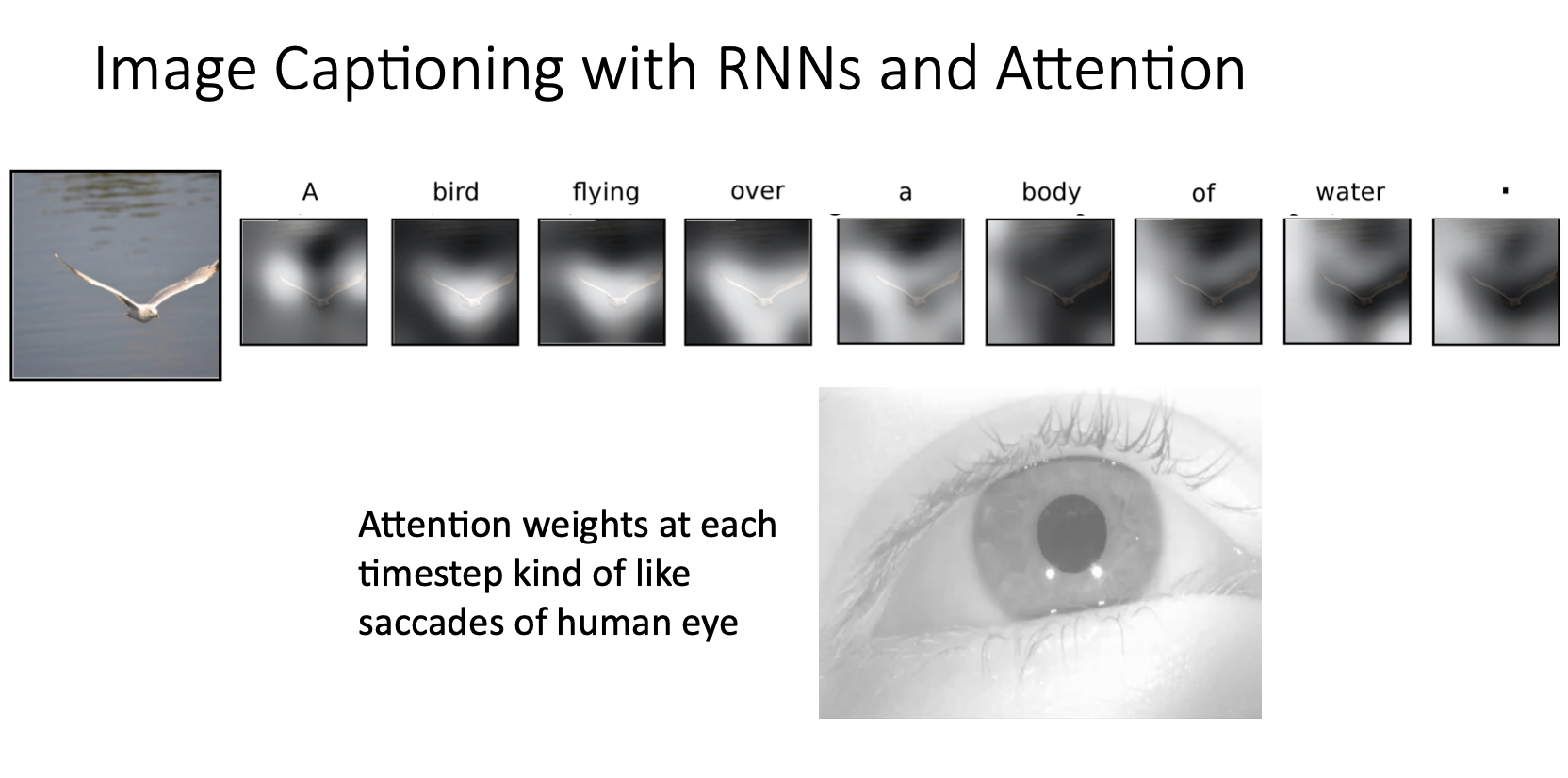
그래서 Attention의 각 step마다 이미지의 여러부분을 빠르게 움직이면서 보는 것을 saccading에서 영감을 받은 것

Attention Layer

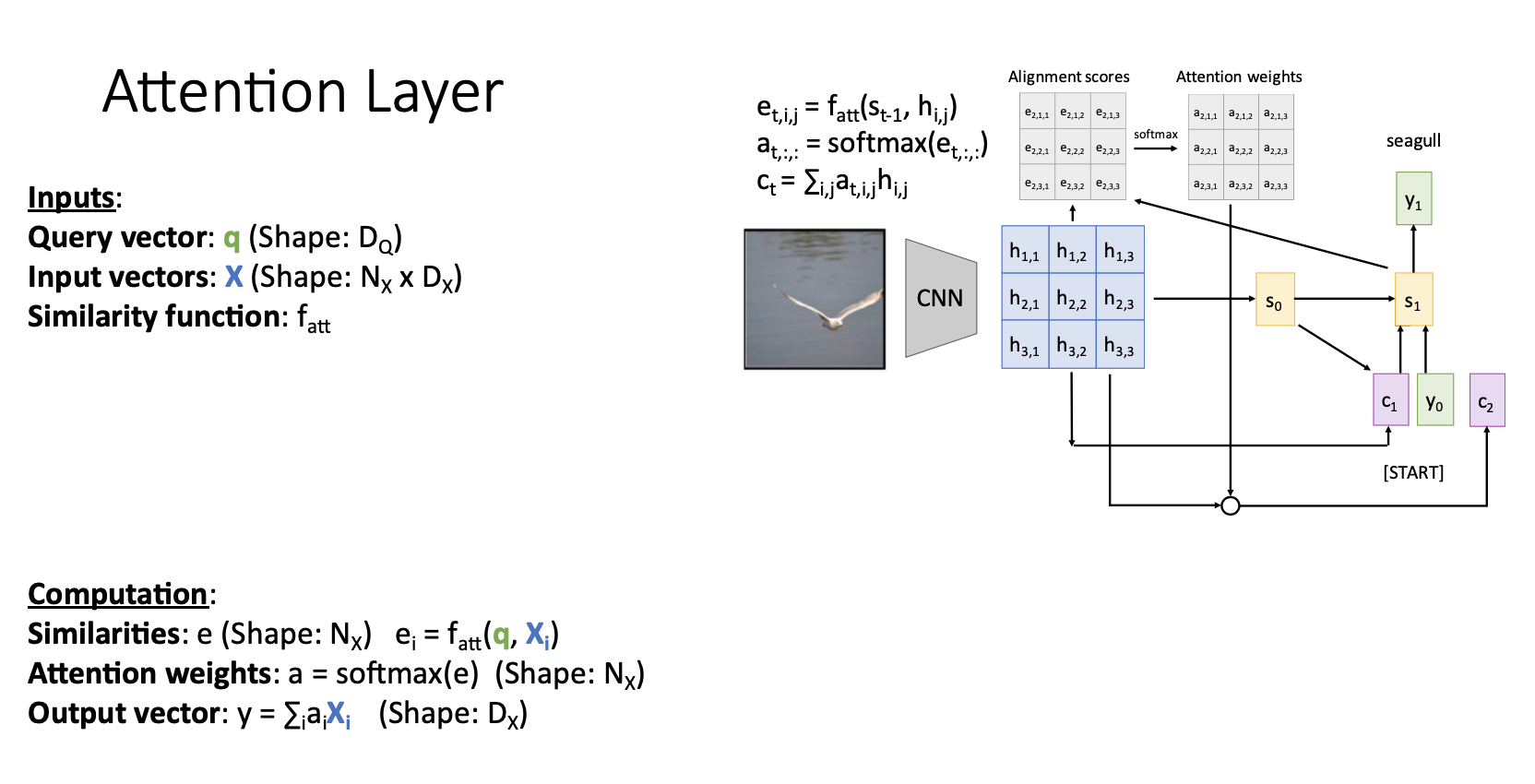
attention mechanism을 attention layer로 일반화하는 과정에서 아래와 같은 방식으로 reframe 시킴
- Inputs
  - Query vector q : decoder의 현재 시점의 이전 hidden state vector (각각이 $s_t-1$ 들이 t시점의 query vector 되는 것 )
  - Input vector X : encoder의 각 hidden state $(h_{i,j})$ 의 collection
  - Similarity function $f_att$ : query vector와 input vector $(h_{i,j})$ 를 비교하기 위한 함수임
- Computation
  - Similarities $e_i$ : query vector q와 input vector $X_i$ 를 similarity function 연산으로 unnormalized similarity scores를 얻음
  - Attention weights $a$ : similary function을 통해서 얻은 $e$ 를 softmax를 거쳐서 Normalized probability distribution을 얻음
  - Output vector $y$ : Attention weights와 input vector를 weights sum $(\sum_i(a_iX_i))$

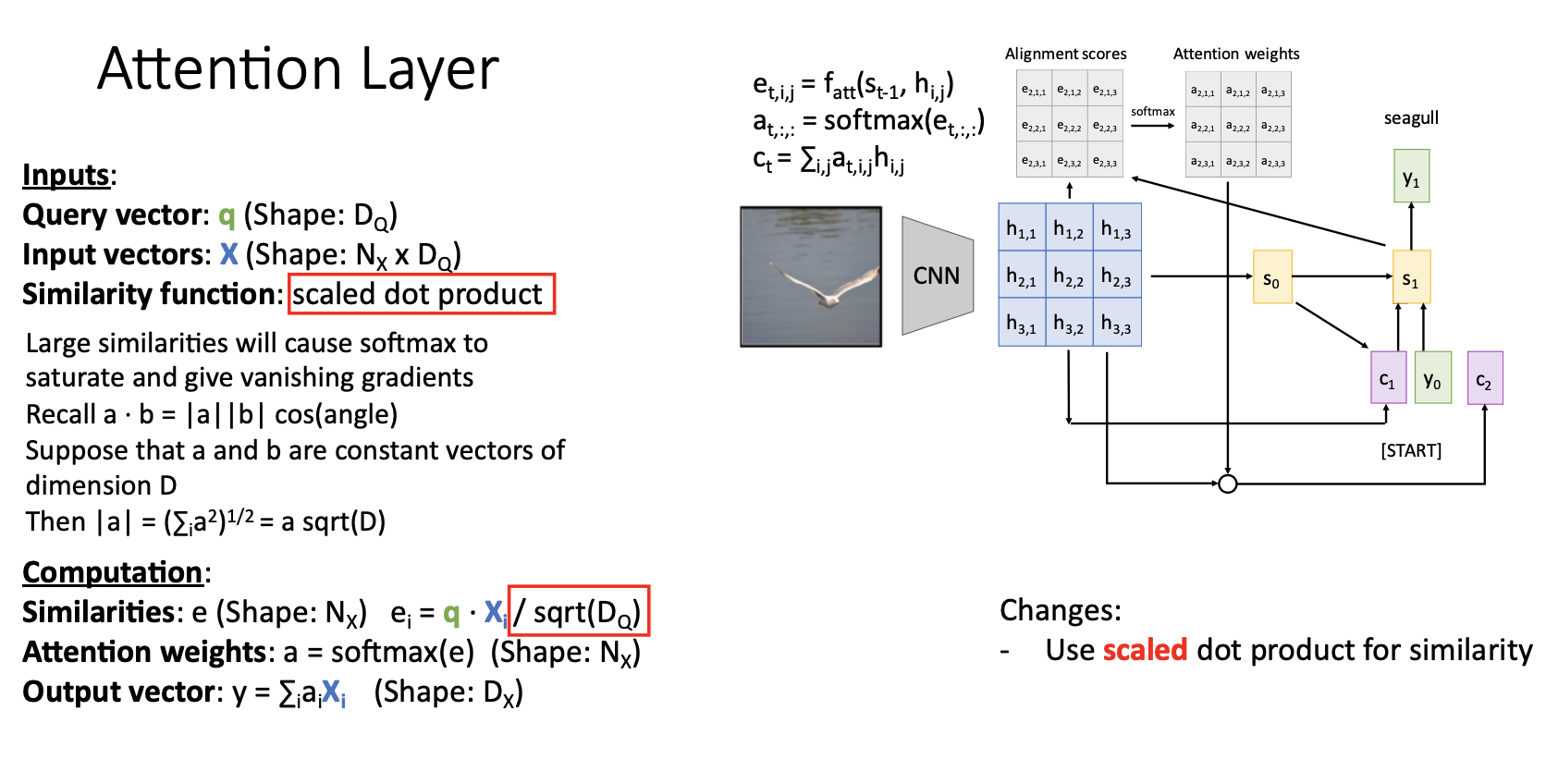
첫번째 generalizaiton으로 Similarity function을 scaled dot product 연산으로 변경해서 matrix multiplication 형태로 연산하여 훨씬 효율적으로 연산함
기존의 $f_att$ : similarity를 계산하기 위해 신경 사용, similarity $e$ 를 신경망의 출력응로 하나씩 계산함
변경된 $f_att$ : scaled dot product 사용. matrix multiplication을 통해서 모든 similarities 한번에 계산할 수 있어서 효율적. scaled는 나누어주는 sqrt($D_Q$)를 의미함. ($D_Q$ 는 input vector $X_i$와 query vector q의 dimension임) . scaled dot product를 사용하는 이유는 similarity scores $e_i$를 softmax에 input으로 넣게 되는데 $D_Q$ 가 클수록 (두 벡터 차원이 클 수록)gradient vanishing 문제가 발생 . 한지점에서만 $e_i$ 값이 엄첯ㅇ 큰 경우에 softmax를 통과하게 되면 그 i지점에서만 높게 치솟은 형태가 되니까 그 부분을 제외한 다른 지점에서의 gradient가 0에 가깝게 됨.

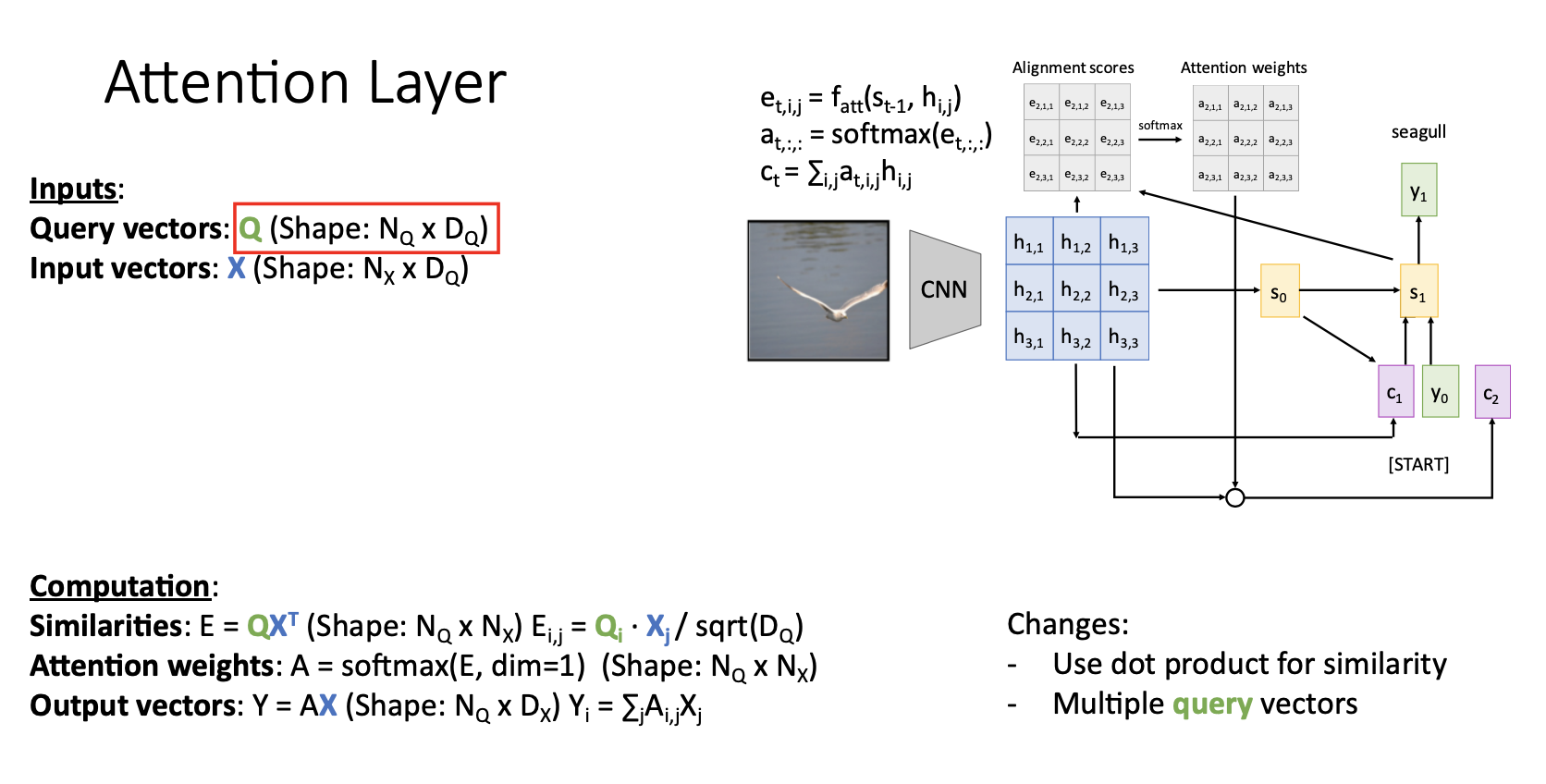
두번 째 일반화 과정으로는 여러개의 query vector를 허용하는 것
기존에 single query vector q를 input으로 받던 것을 set of query vector Q로 받아 모든 similarity socores를 single matrix multiplication operation으로 모든 연산에서 한번에 계산 (similarity function이 내적으로 변경되었기 때문에)

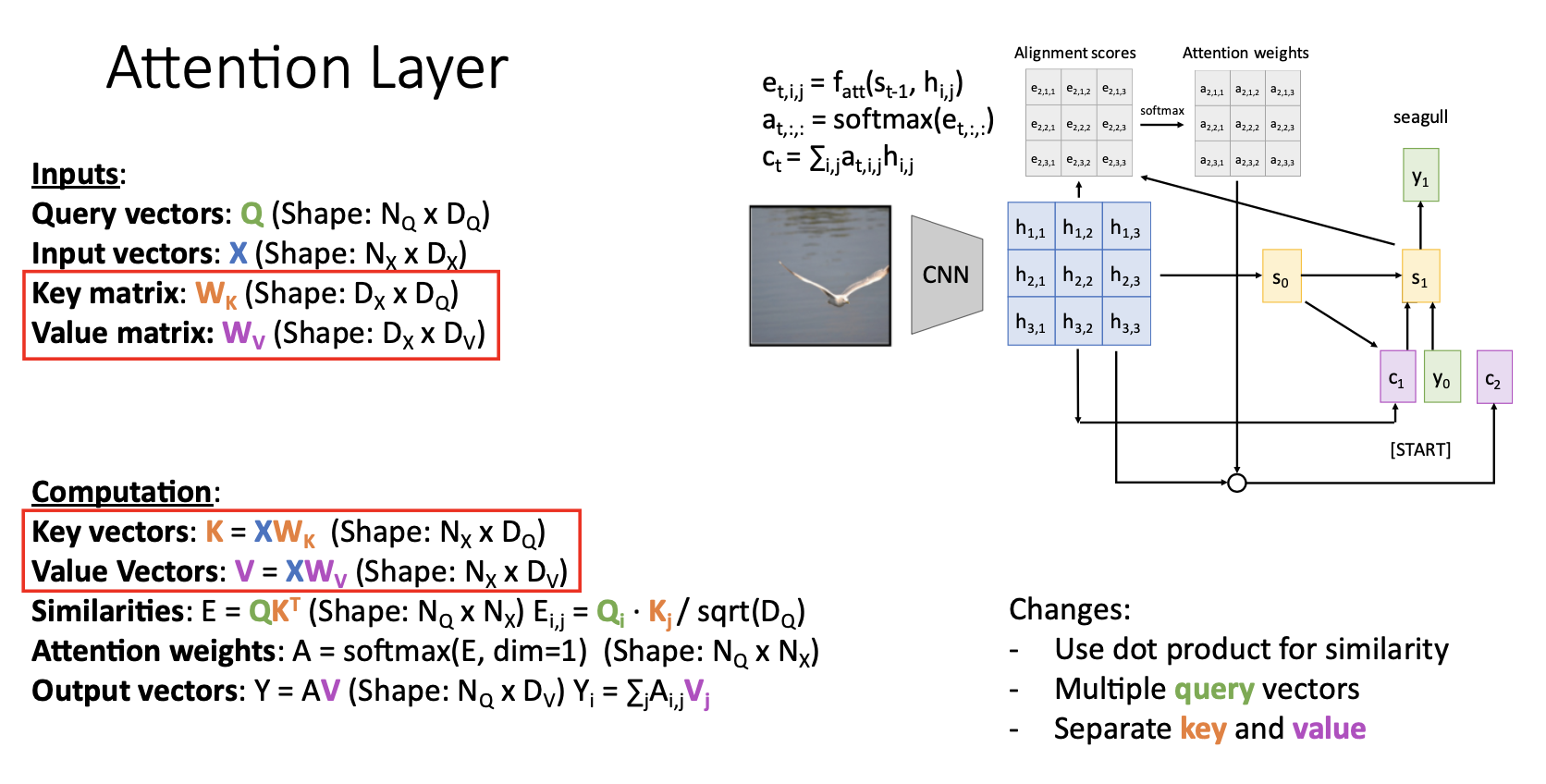
세번 째 일반화 과정은 similarity와 output을 계산할때 동일하게 사용되던 input vector X를 각각 Key vector K와 Value vector W로 분리하는 것이다.
예를 들어 구글에 엠파이어 스테이트 빌딩의 높이라고 검색을 한다고 하면 검색한 문장인 엠파이어 스테이트 빌딩의 높이가 query가 되고, 원하는 정보를 얻을 수 있는 웹페이지가 ouput이 됨
우리가 원하는 건 빌딩의 높이를 알려주는 웹페이지이고, 이는 검색한 문장(query)과는 무관한 데이터라고 생각할 수 있음

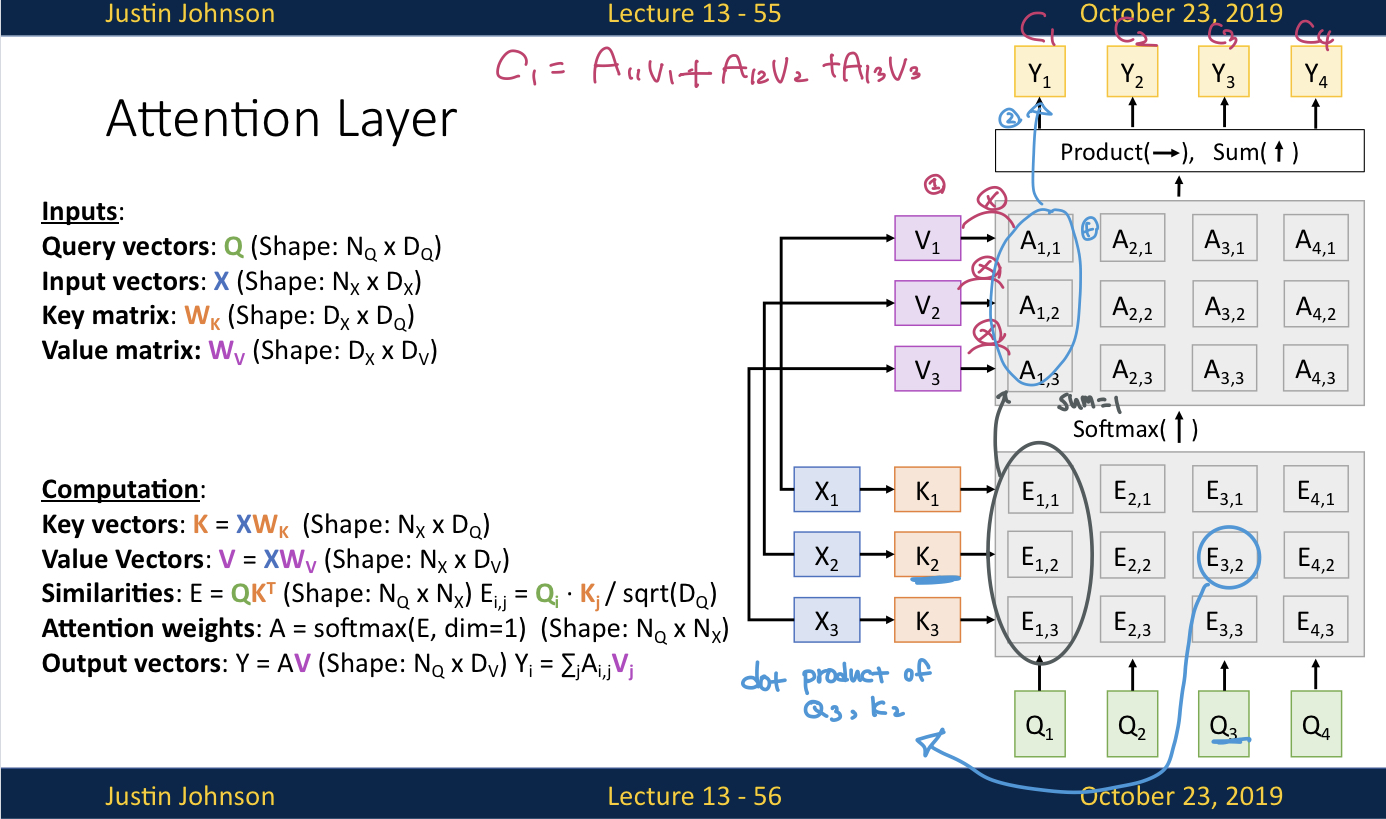
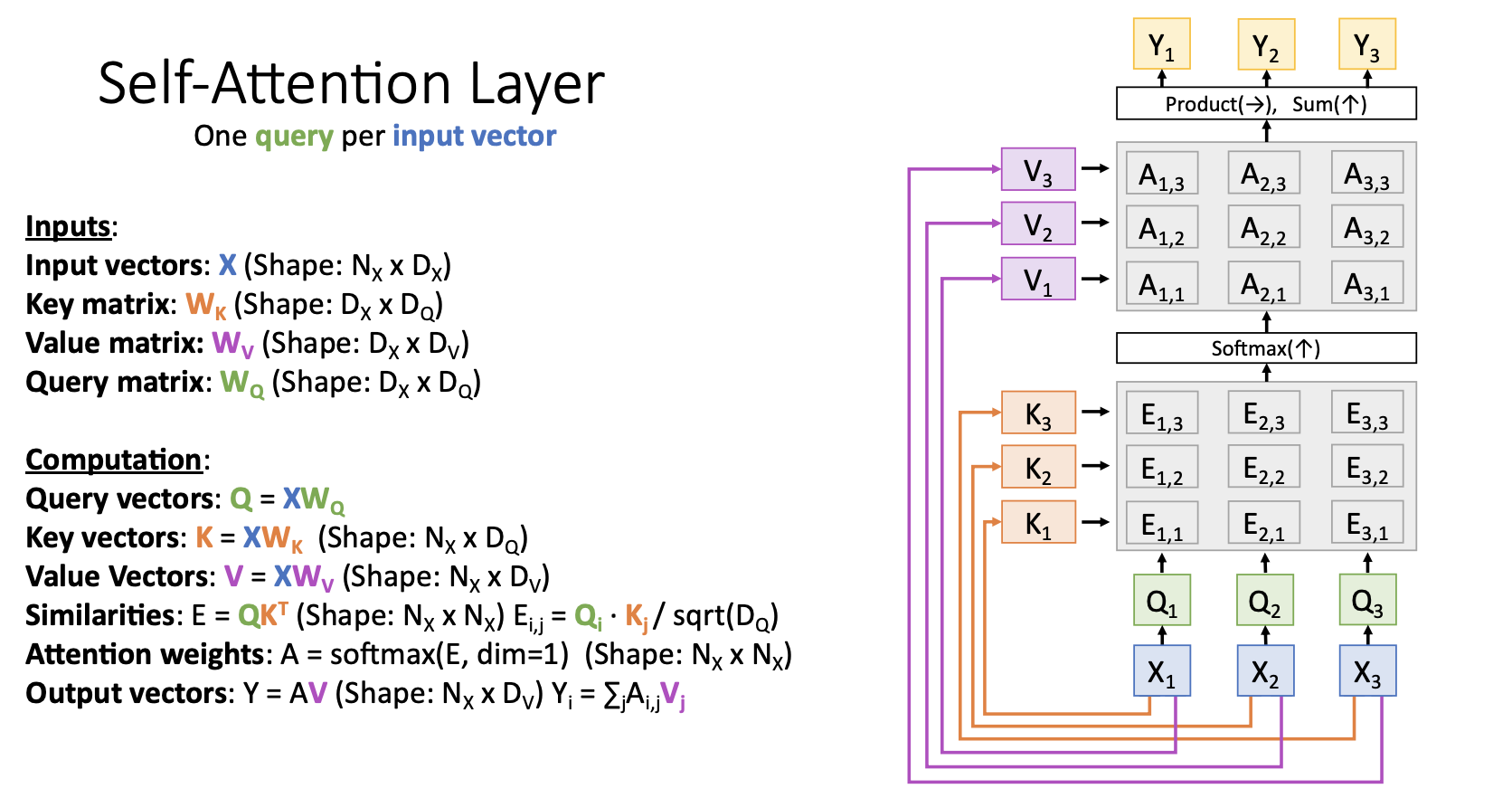
지금까지 살펴본 변경사항들을 적용한 Attention layer는 위 그림과 같이 동작함
$ X_1, X_2, X_3$ 에 해당하는게 $h_1, h_2, h_3$ 엿음
query vector는 output문장의 hidden state 였음 ($s_0, s_1, s_2, s_3 $)
input vector $ X_1, X_2, X_3$ 를 통해서 key vectors $K_1, K_2, K_3$ 를 생성함
query vectors $Q_1, Q_2, Q_3, Q_4$ 와 Key vectors $K_1, K_2, K_3$ 를 통해서 similarity matrix E를 생성함
$E_{i,j}$ : dot product of $Q_i, K_j$
similarity matrix E를 softmax에 통과시켜서 attention weight matrix A를 생성함. softmax에 수직방향으로 위로 통과시킨다고 생각
input vectors $X_1, X_2, X_3$를 통해서 values vectors $V_1, V_2, V_3$ 생성
attention weights $ A_{1,1},…, A_{4,3} $ 와 $V_1, V_2, V_3$ 를 통해서 output vectors $Y_1, Y_2, Y_3, Y_4$ 를 구하고 출력

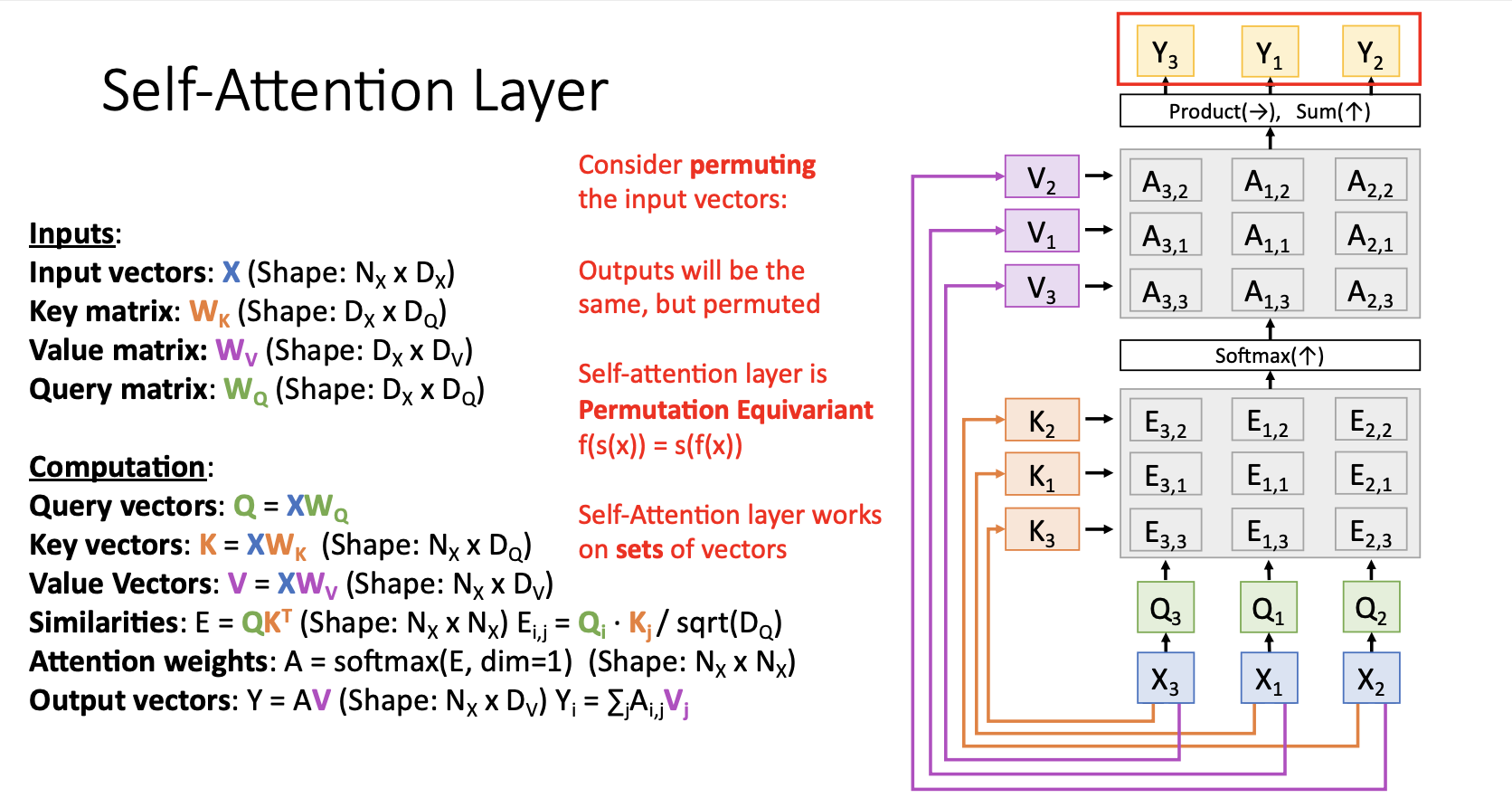
Self-Attention Layer

Attention Layer의 특별 case인 Self-Attention Layer는 input vector set을 입력받아서 각 input vector들끼리 비교하는 형태이다. (입력한 문장 내의 각 단어를 처리해 나가면서 , 문장 내의 다른 위치에 있는 단어들을 보고 힌트를 받아 현재 타겟 위치의 단어를 더 잘 인코딩할 수 있게 하는 과정)

PREVIOUSLecture 12. Recurrent Neural Networks

NEXTLecture 14. Visualizing and Understanding