Training Neural Network
Activation Functions
Activation function은 linear하게 프로세싱된 것를 f가 non linear하게 구부러뜨림. f가 linear하다면 네트워크 깊게쌓는 의미가 없음.

sigmoid

확률적인 해석이 가능. s자. 예를 들어 0.8이 나오면 다음 레이어를 활성화 시킬 확률이 0.8 이런식. 하지만 크게 세가지의 문제.
-
Saturated neurons(x값이 크거나 작다) kill the gradients
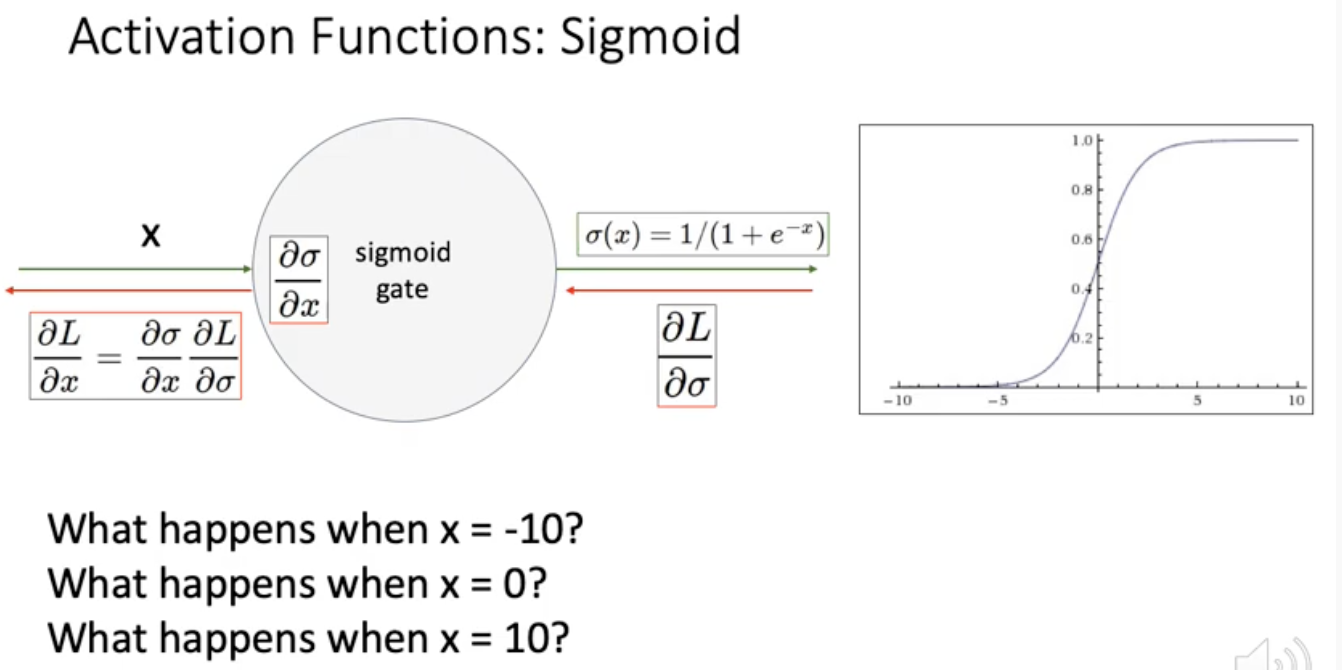
x가 -10이거나 10일때 downstream gradient가 거의 0. 누적되면 아랫단 레이어에 실제적으로 업데이트 돼는 그래디언트 양이 미미. 그래디언트가 너무 작으면 W가 업데이트되는 양이 거의 없음. 그래서 train이 거의 안됨. -
Sigmoid outputs are not zero-centered

W쪽의 Local gradient계산해주면 x가 전부. 그니까 전부 positive or negative. 부호를 절대 바꾸지 않음. 지그재그 반복해서 W가 업데이트. 근데 실제적으로는 Minibatches가 도와주기 때문에 글케 심각한 문제는 아님

-
exp() is a bit compute expensive
Tanh

시그모이드 위아래로 늘린 형태.. 뭐가 좋냐면 output이 0을 중심으로 퍼져있음. 그래서 single element에 대해서 W의 direction이 다양할 수 있다. 하지만 여전히 saturated된 value가 input으로 들어오면 downstream gradient가 kill될수 있다는 위험
ReLU
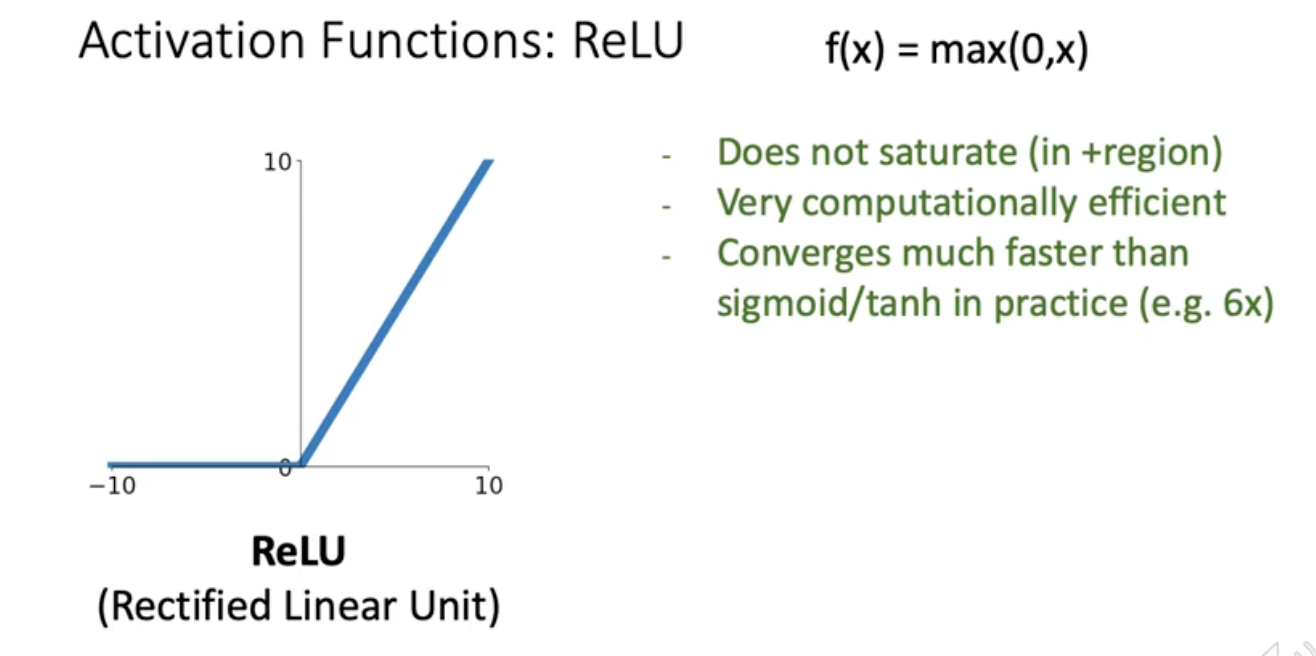
이녀석은 0보다 큰 곳에서는 gradient가 정확하게 1. input이 positive라면 downsteram gradient가 Kill되는 일은 없음. 또한 컴퓨터 연산이 빠른 단점이 있음.
그럼데도 relu도 잠재적인 위험이 있음. sigmoid 처럼 output이 non negative임.
Leaky ReLU

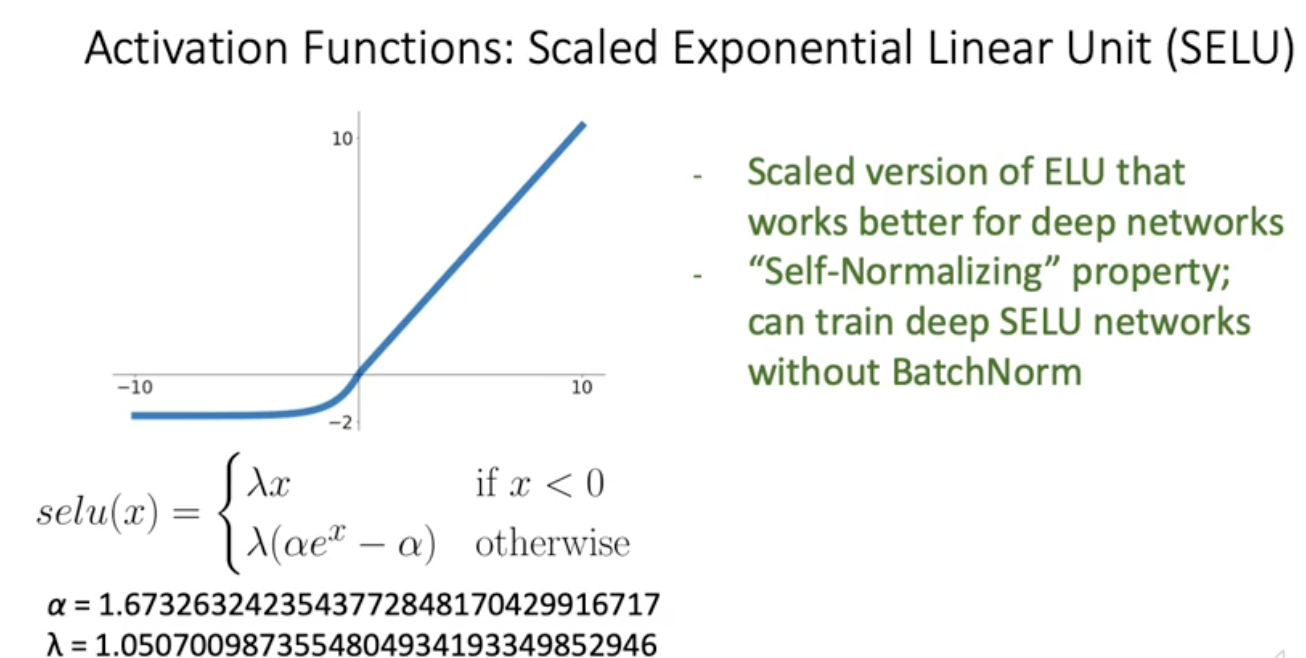
SELU
Accuracy
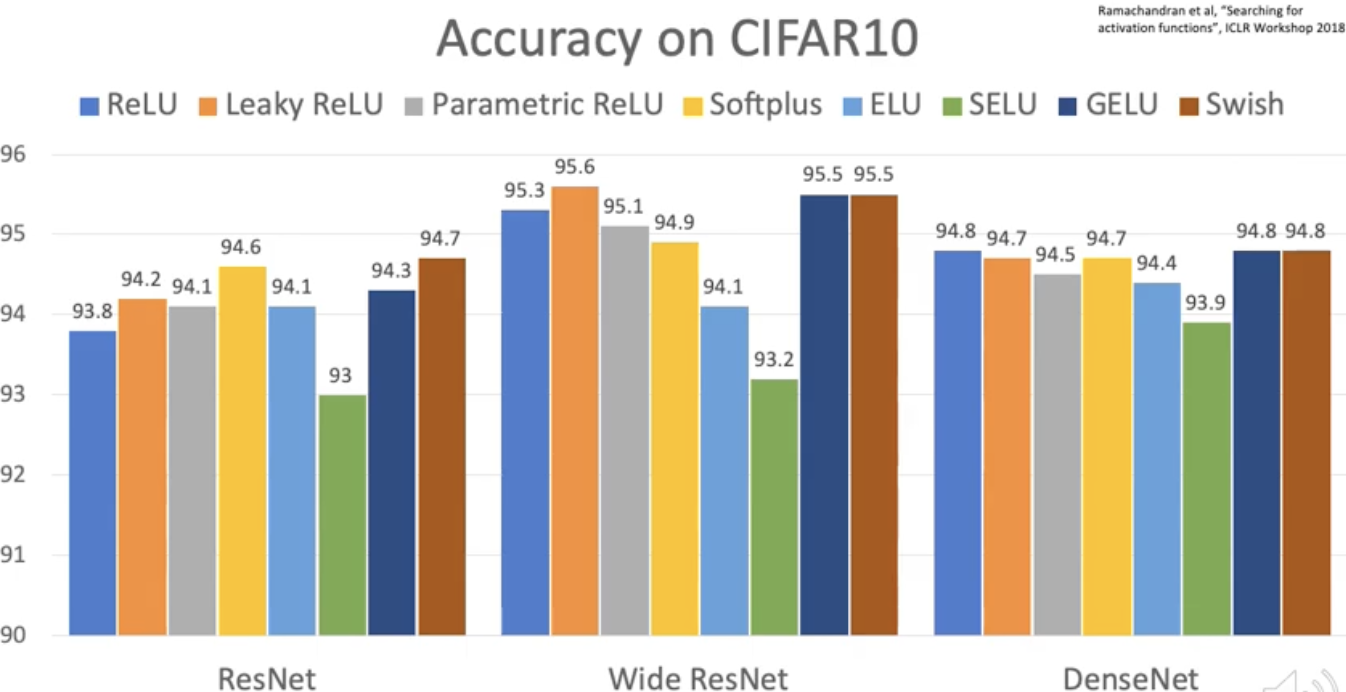
결론은 걍 relu 쓰라는거. 그리도 sigmoid나 tanh activation은 쓰지 말라.
Data Preprocessing
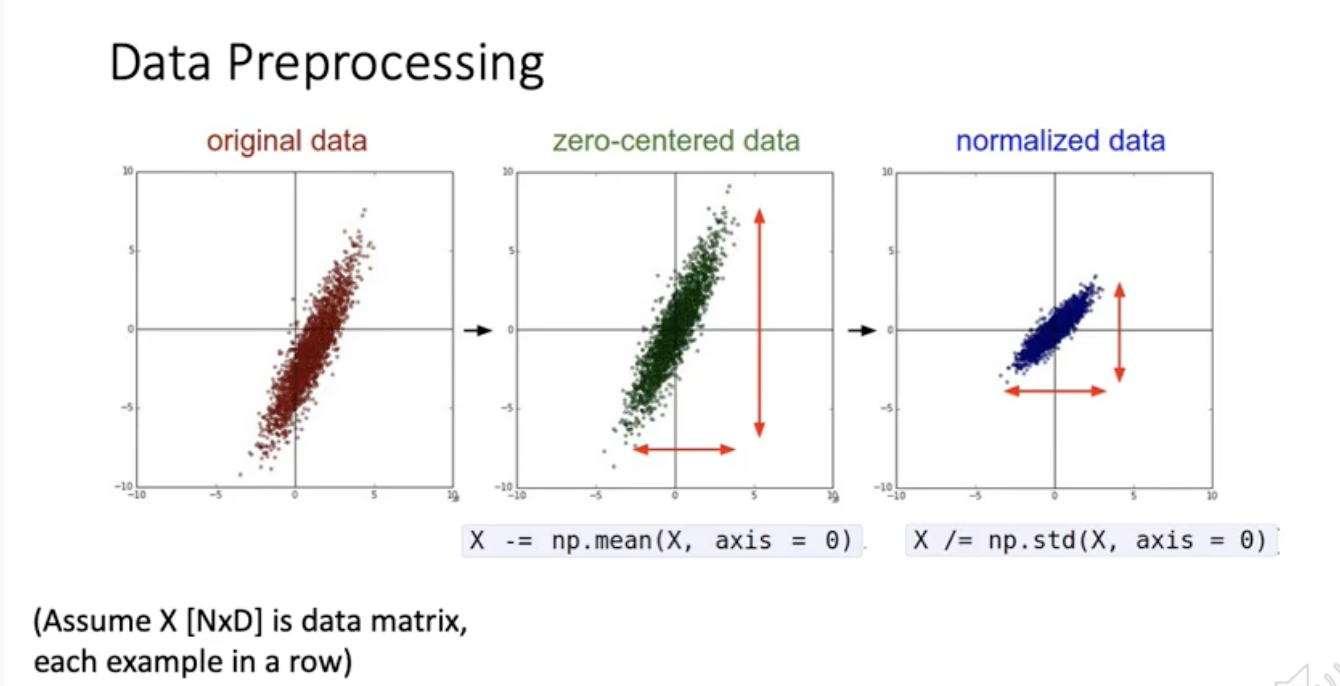
이걸 굳이 하는 이유? 이론적으론 유리하지 않지만 practical에는 유리. gradient시에 normalization 하는게 유리.
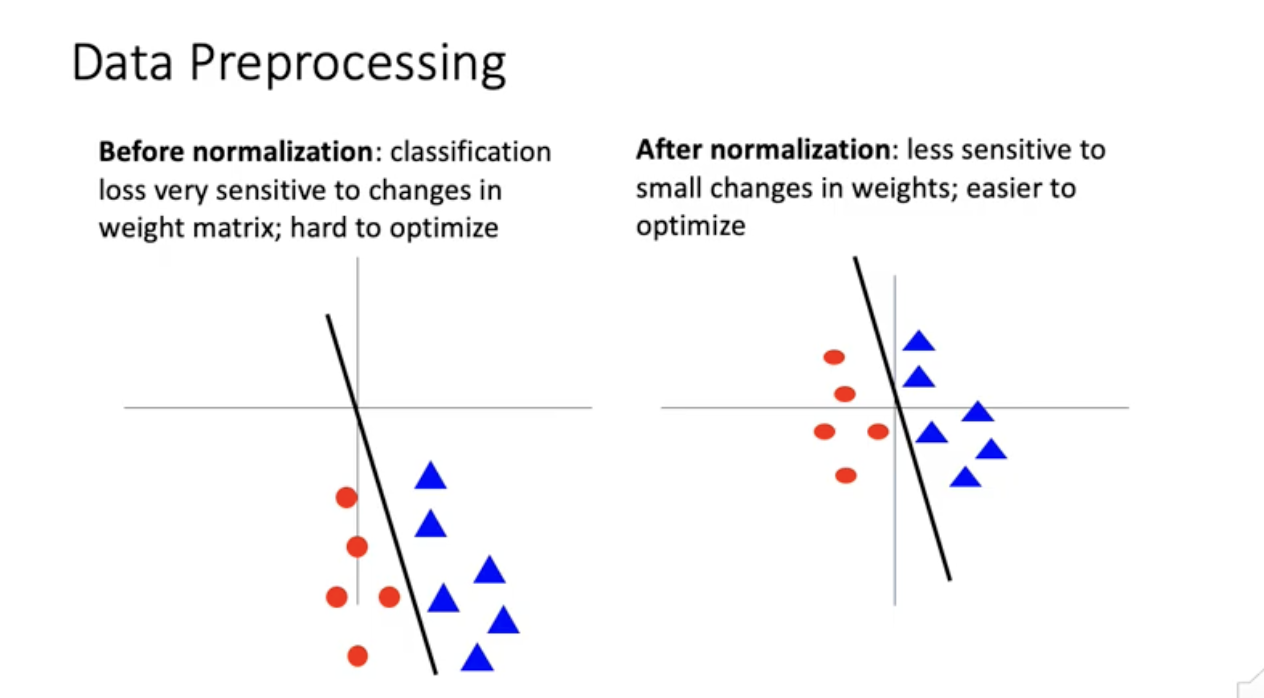
위의 그림을 보면 normalization하지 않았을 때 slope가 조금 변하더라도 영향을 많이 받음. weight matrix가 조금만 바껴도 classification loss가 아주 많이 바뀜. 간접적으로는 Optimization process를 어렵게 만들 수 있음. normalizaition한 후 원점에 위치하면 weight 변경에 조금 덜 민감. 선형회귀분석에서도 표준화한다고 해서 loss function의 minimum이 바뀌는 것은 아니지만 최적화 문제가 더 빠르게 수렴이 가능.
Weight Initialization
non-convex 문제에서는 initialization을 잘 해야됨.
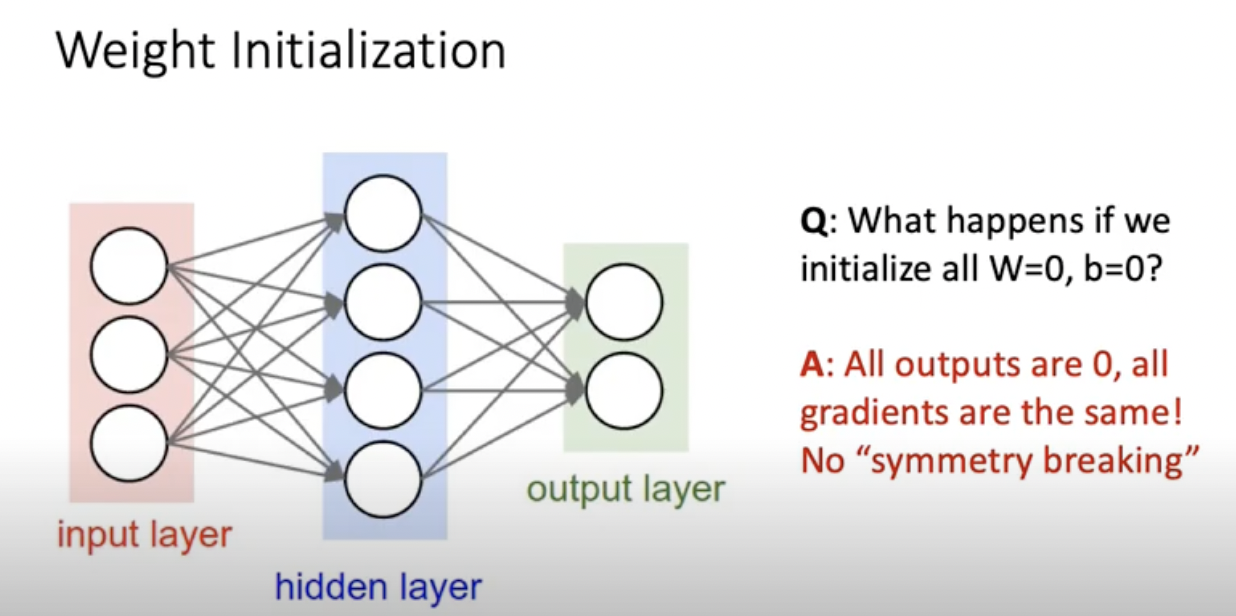
Weigth 와 b가 모두 처음에 0이라면 output이 0 이되어 gradient가 모두 같아짐. 대칭성을 깨줘야 학습이 되는데 이렇게하면 학습이 안됨. W와 b가 조금씩 달라야됨.
기본적으로 neural network구조는 각각의 hidden layer에서 node들의 역할이 모두 대칭적인데 all zero로 초기화를 하는 순간, 대칭적인 역할을 깰수가 없게 된다.
그래서 많이 쓰는 방법이 input 개수,out 개수 만큼의 random number generate해서 0.01 곱해줌. 작은 네트워크에서는 이렇게 하는게 잘 작동을 하는데 깊은 네트워크에서는 문제가 발생

6레이어 뉴럴네트워크를 만들고 각각의 레이어의 사이즈는 4096임. 그다음에 x는 16x4096으로 초기화. 그다음에 for문으로 forward pass를 한번만 돌림.
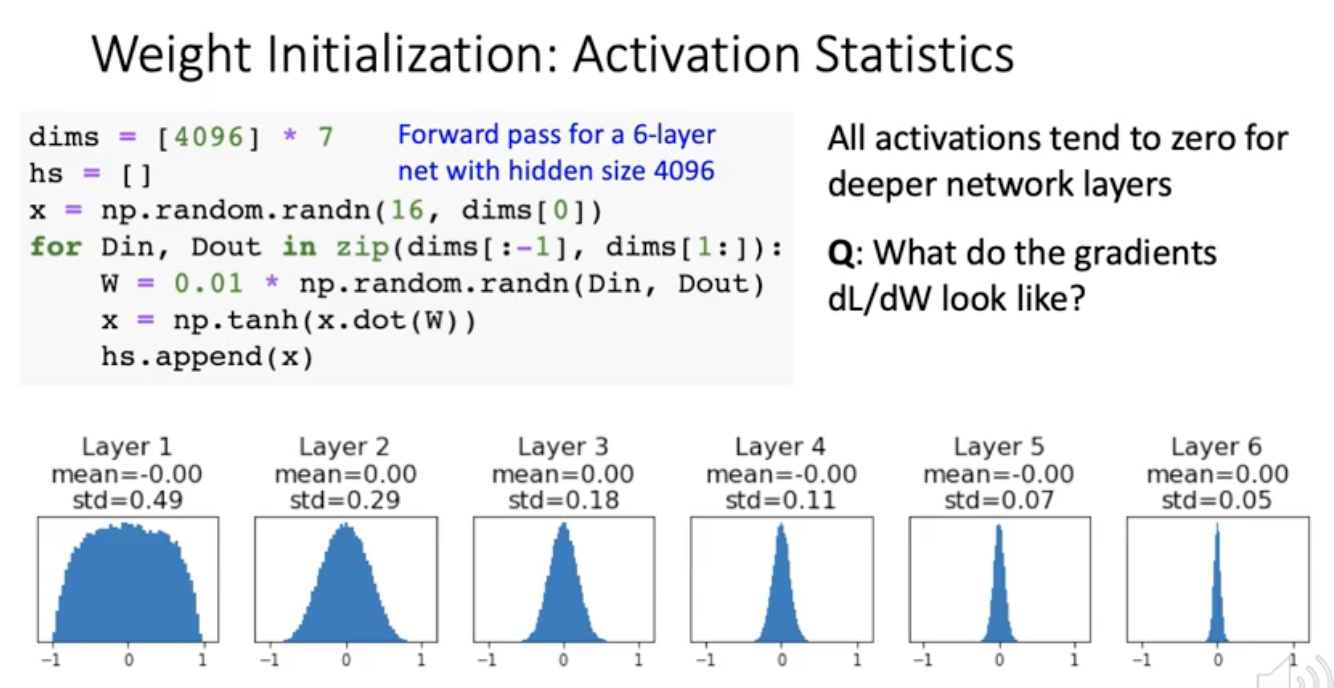
x를 histogram으로 그려보니 처음에는 잘 퍼져있는데 레이어가 올라갈수록 0쪽으로 squeeze가 됨. activated 값의 분포가 layer가 올라가면서 점점 균질하지가 않아. 그러면 backpropagation할때 무슨 문제가 생기냐면 x의 분포가 초장부터(layer6) 0근처에서 거의 벗어나지 않음. 이러면 training이 거의 안됨.
그러면 weight 초기값 조금 더 퍼뜨리면 되나 ?
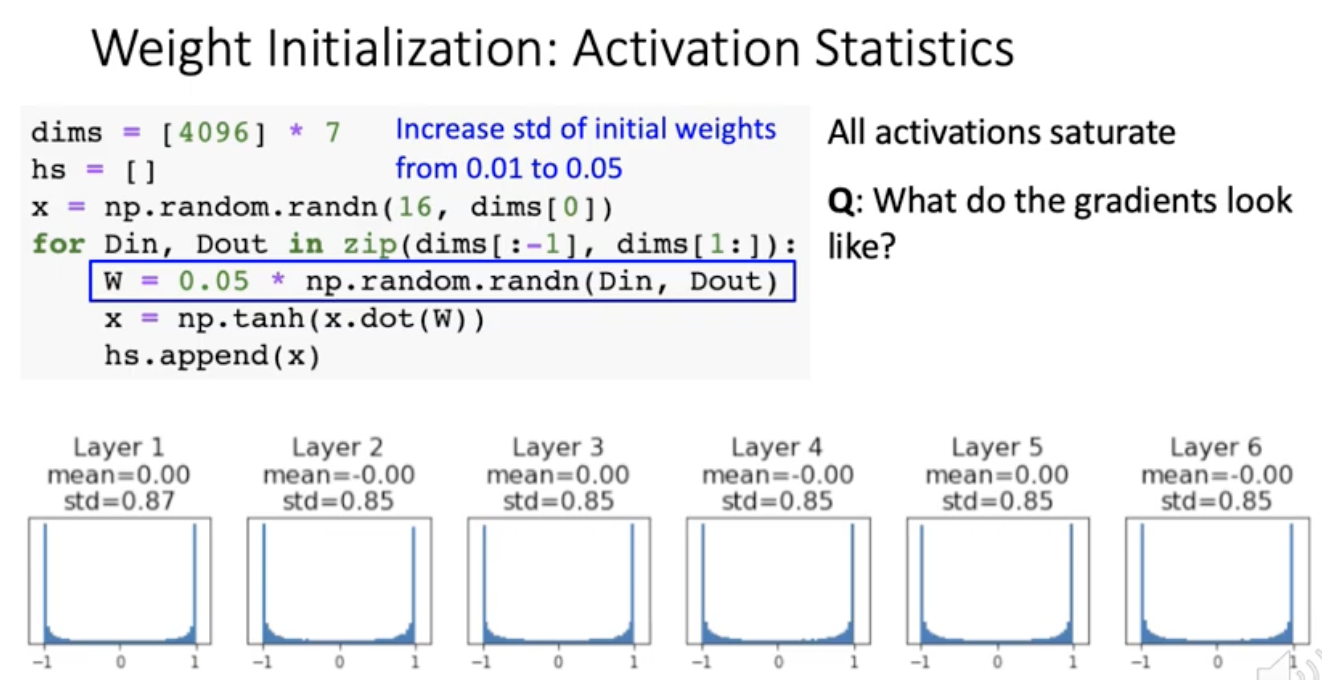
tanh함수에서 -1과 1근처에 있던 것은 gradient가 0이었음. 그러니까 local gradient가 또 0 근처.
그러면 어케해야됨? -> Xavier Initialization
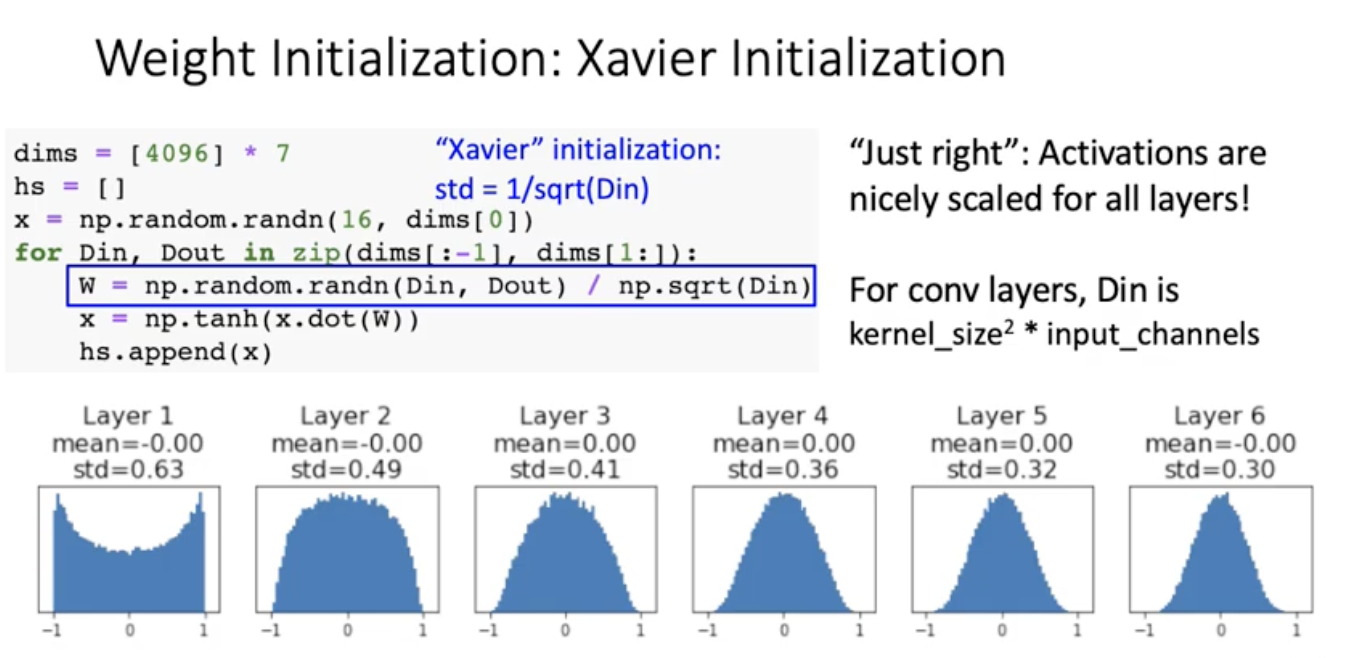
아주 간단한 상황에서의 직관에서 나옴.
Xavier initialization
input node들의 activation의 variance과 output node들의 activation값들의 variance이 같도록.
y= Wx 에서 y=(4096,1), W=(4096,4096), x=(4096,1). one sample에 대해서 hidden node들의 관계를 쓴거. output yi하나는 j=1부처 4096까지 갈때 xj 스칼라 하나하나랑 W매트릭스에서 로우 한줄 떼서 내적. 그다음에 x랑 w가 independent하다는 가정을 하면 저 variance를 뺄 수 있음. 그 다음에 x와 w의 평균이 0이면 평균제곱이 다 날아가고 x의 Variance와 W의 variance로 나타낼 수 있다. 이때 W의 variance를 1/Din으로 설정해주면 Din이 cancel out이 되가지구 yi의 variance와 xi의 variance가 같게됨.
그르면 ReLU에서는 ? 잘 통함?
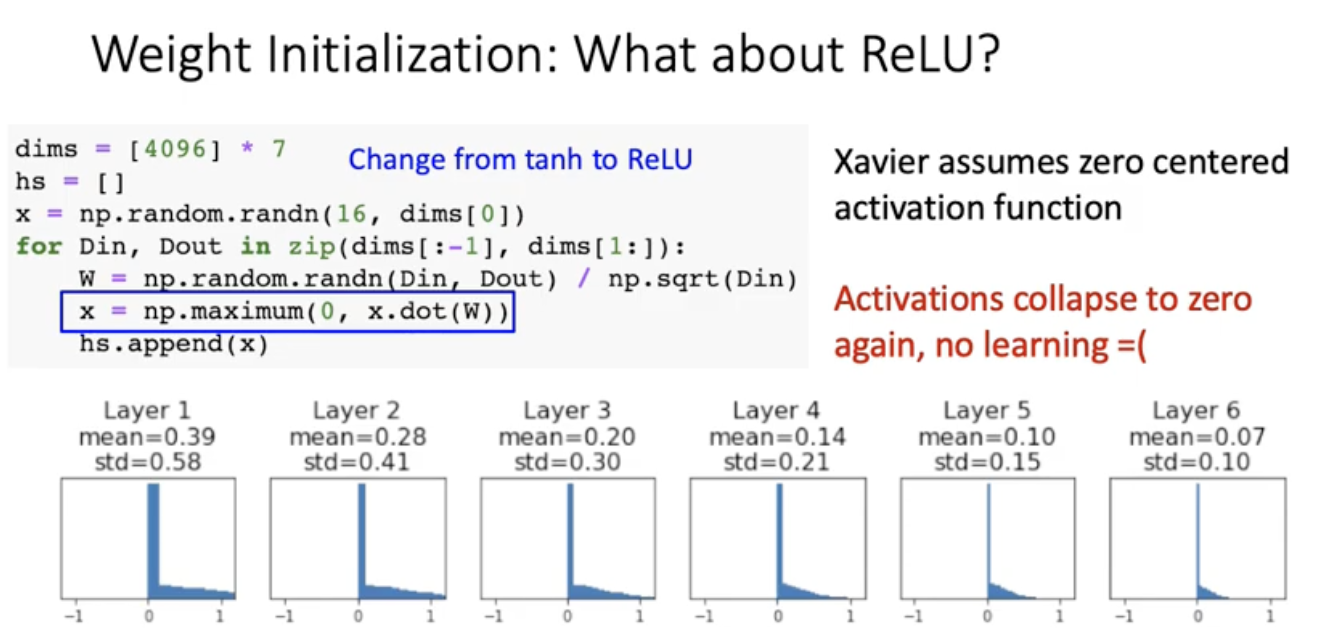
또 0으로 모이는 현상이 관찰. learning이 이뤄지지 않음.

이렇게 2를 곱해준다. 이걸 Kaiming initialization/MSRA Initialization이라고 한다.
Weight Initialization : Residual Networks
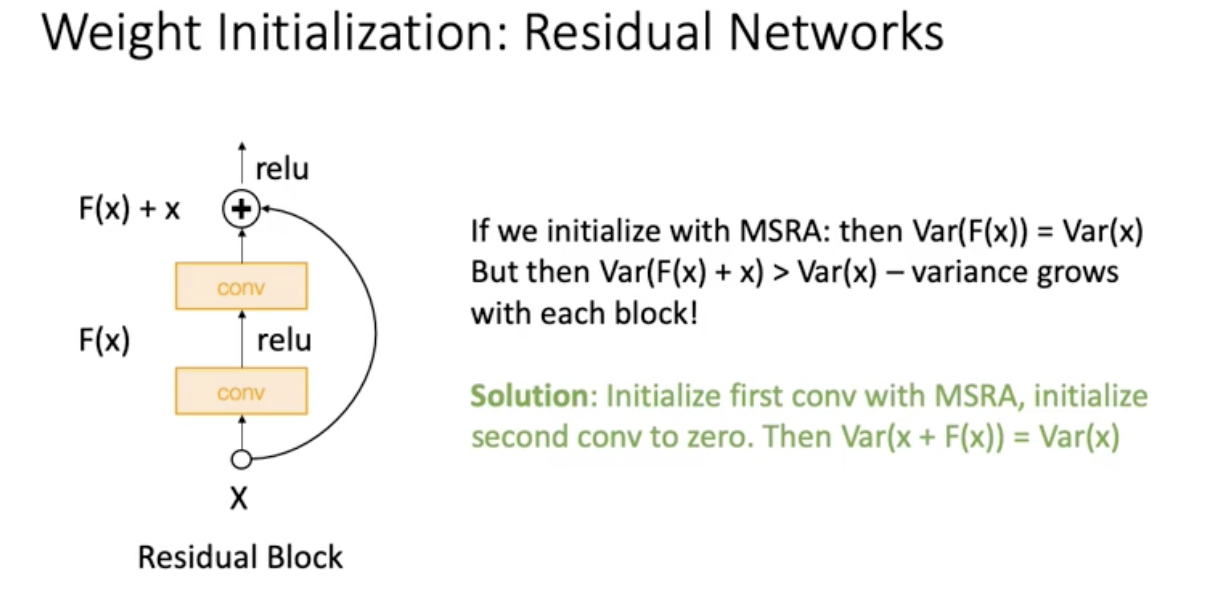 MSRA Initialization사용하면 residual에서는 Var(F(x)+x)>Var(x) 라는 문제가 생긴다. 그래서 이를 해결하기 위해서 Var(x+F(x))=Var(x)로 설정해줌
MSRA Initialization사용하면 residual에서는 Var(F(x)+x)>Var(x) 라는 문제가 생긴다. 그래서 이를 해결하기 위해서 Var(x+F(x))=Var(x)로 설정해줌
Regularization
학습을 방해하는 역할을 함

Dropout
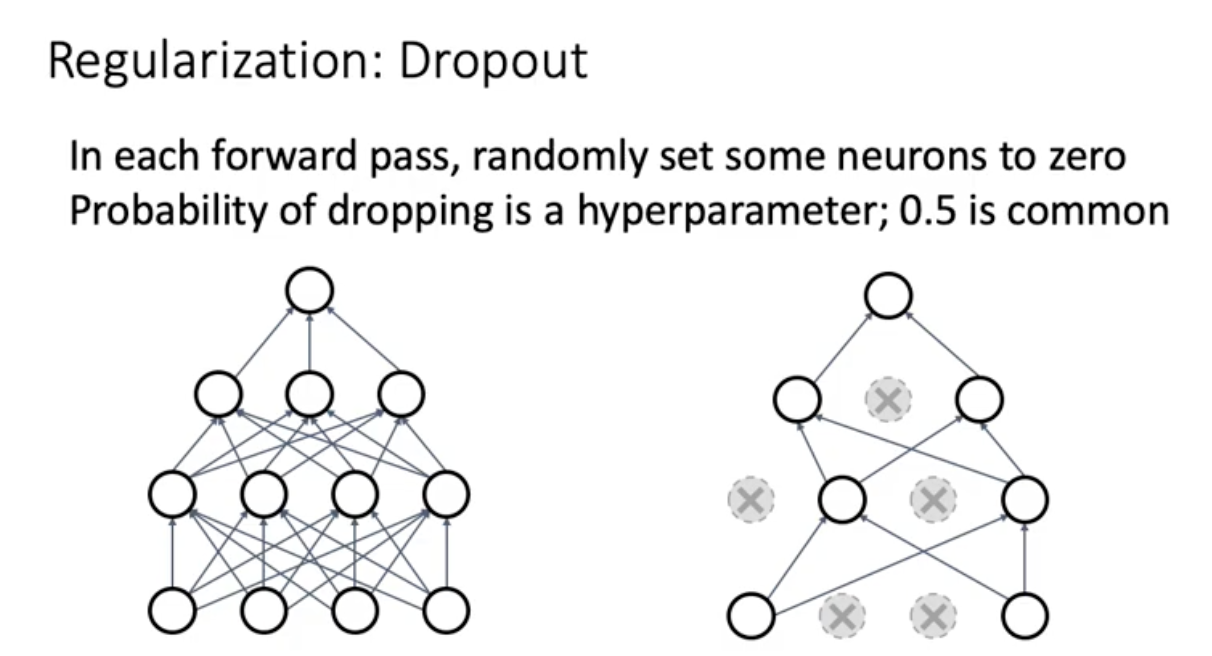
중간 중간 옆에 노드가 없다보니가 뉴런 하나하나가 잘 배워야됨. x의 표현을 배운다. 필요없는 건 덜 배움.
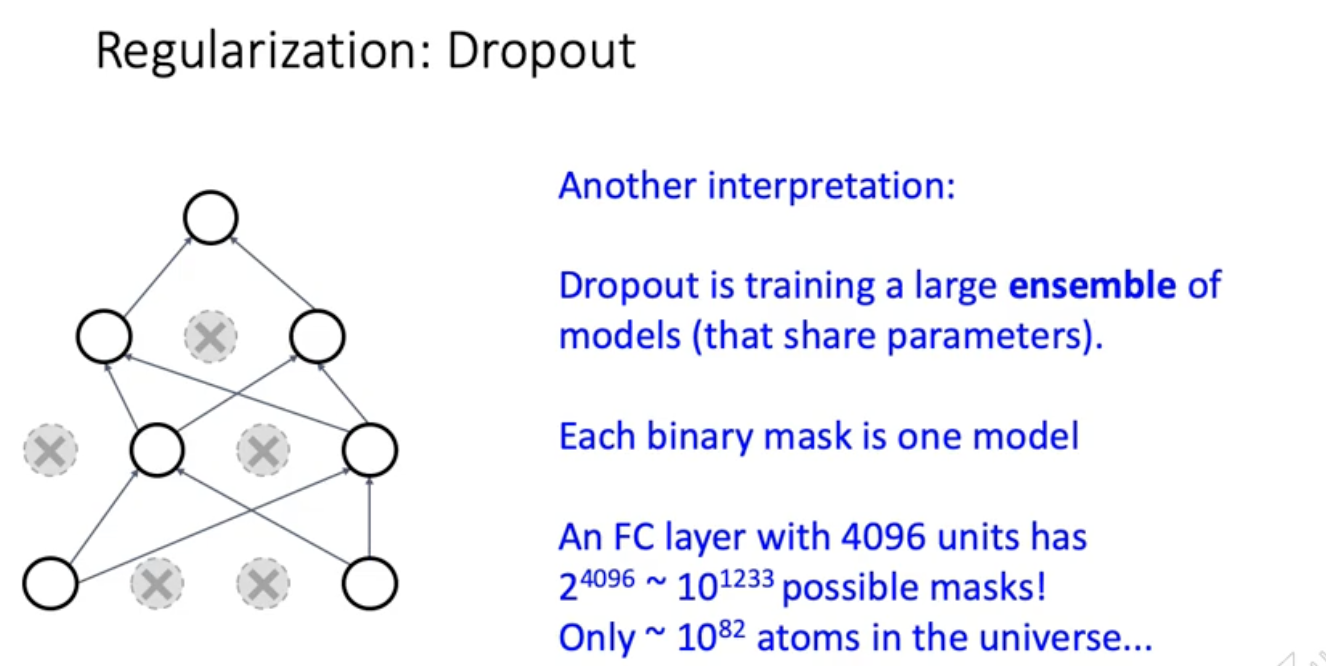
dropout은 매 iteration마다 sub neural network를 training하는 과정. 전체 네트워크는 subnetwork들의 앙상블.

testing할때는 z가 random하면 고정된 W,X에 대해서 결과가 달라짐. 사람들이 안좋아함. 그래서 z의 probabilistic distribution p(z)에 대해서 Integrate out 하고 싶어함. 평균 내고 싶어하는거.근데 연산량이 너무 많음.
그래서 Integraldmf approximate하고 싶어함



train할때 미리 tuning해주고 test할때는 아무것도 안함
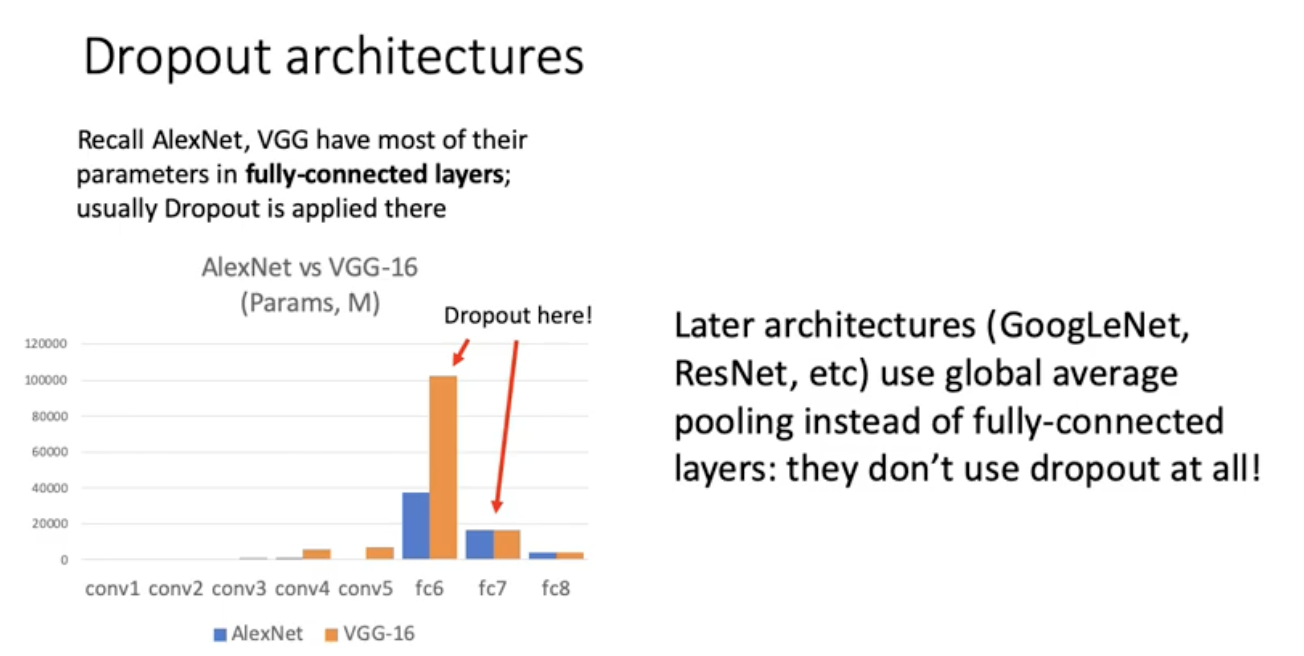 요즘 dropout 잘 안쓰는 이유는 googlenet이런거에선 Fully connected layer 많이 안씀. 따라서 dropout쓸일이 별로 없음. VggNet이나 Alexnet같은 예전 아키텍처 쓸ㄷ때 사용
요즘 dropout 잘 안쓰는 이유는 googlenet이런거에선 Fully connected layer 많이 안씀. 따라서 dropout쓸일이 별로 없음. VggNet이나 Alexnet같은 예전 아키텍처 쓸ㄷ때 사용
정리 ! : For ResNet and later, often L2 and Batch Normalization are the only regularizers.
Data Augmentation
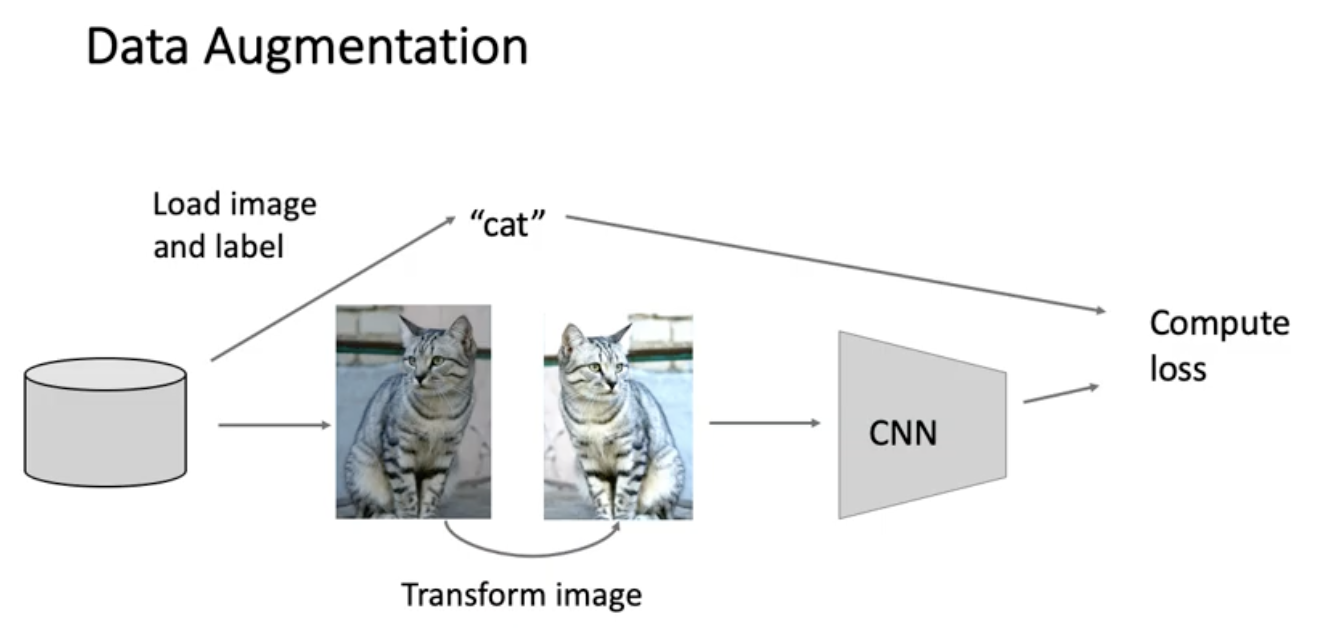
샘플 사이즈가 부족할때는 training 성능 높여주기 위해 augmentation 함.


training 시에는 임의의 정수 L을 선택해서 늘려준담에 거기서 224x224를 빼냄
testing 시에는 test용 이미지를 5개의 scale로 만든 다음에 거기서 224x224를 10개씩 코너 4개 센터 하나, 뒤집어서 5개 뽑은 다음에 10개에 대한 classification 결과를 투표시켜서 predict 함.

이외에도 DropConnect
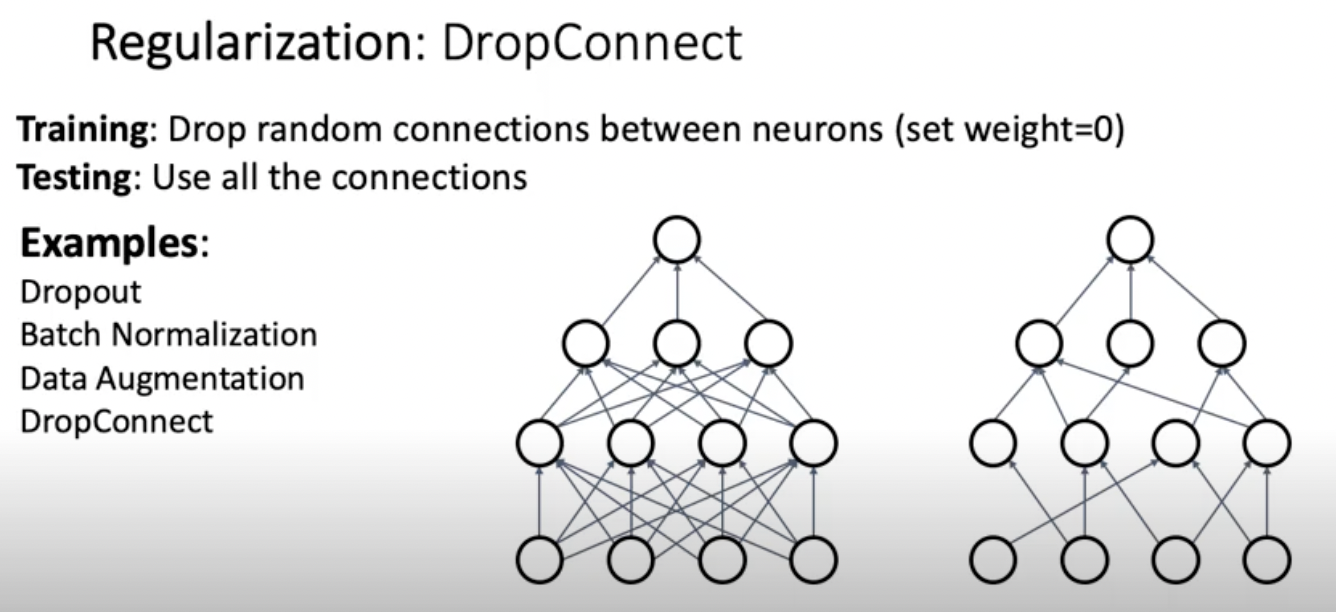
fractional pooling : downsizing영역을 랜덤하게 가져하는 거

stochastic Depth : resnet에서 랜덤하게 몇개의 residual block 쌩깜

Cutout : 이미지에서 조금씩 랜덤하게 사각형 지정해서 0로로 만듬

Mixup

아직도 많이 쓰는 건 Batch Normalization이랑 Data Augmentation. 그리고 최근에 Cutout이랑 Mixup도 고려할만하다..