Convolutional Network

이전까지 보았었던 linear classifier와 neural network model은 pixel값들을 flat하게 펼쳐 연산했기 때문에 image의 spatial structure까지 다루지 못한다는 문제점이 있었다. 이 전 강의영상에서 보았떤 matrix valued backprop도 matrix form으로 연산을 하지만 결국 flat한 것과 다를바 없어 spatial feature를 커버하지 못한다. 이러한 문제를 해결하고자 fully connected neural network에 새로운 operator를 정의하여 2-dimensional spatial dadta인 image에 적용하려한다.

Fully-Connected Layer

우리가 이전에 보았던 Fully connected Network는 크게 두가지 구조로 나뉘는데 input vector와 matrix multiply를 해주어 output vector를 내놓는 fully connected layers와 non-linear한 데이터를 linear하게 transform해주는 Activation function으로 구성되어 있었다.

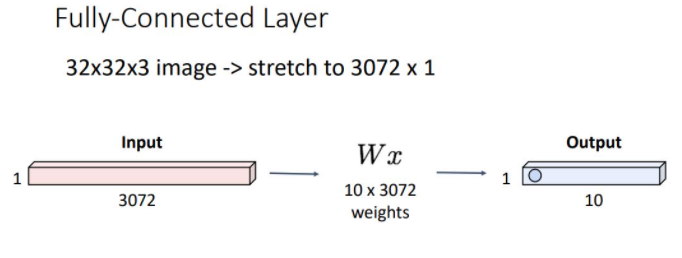
위 그림처럼 이전에 보았던 fully connected layers의 forward pass과정에서 32x32x3 이미지를 3072개의 scalar element를 갖는 vector로 펼쳐 각 class의 weights matrix와 multiplication해주어 output vector를 뽑아냈었다.

Convolution Layer

위 그림에서 convolution layer의 input은 더이상 flattened vector를 사용하지 않고 image matrix와 같은 form인 3-dimensional tensor를 사용한다.
가로,세로를 각각 width와 height라고 하고 폭을 depth 또는 Channel이라고 한다.
weight matrix는 일정의 3-dimensional structure를 갖는데 이러한 weight matrix를 filter라고 한다. 이때 filter는 input image와 같은 크기의 channel을 갖고 image의 모든 spatial position을 돌아다니며 dot product연산을 한다.

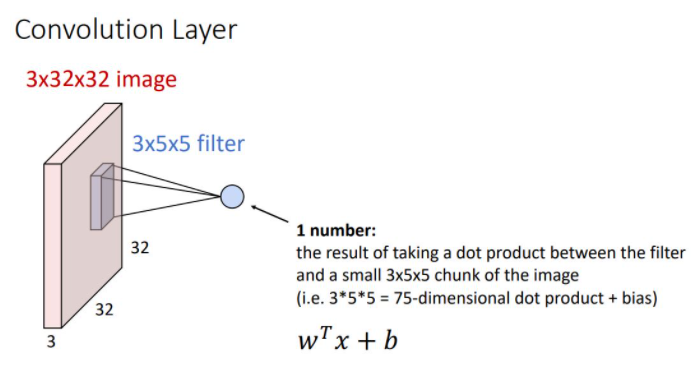
이러한 image의 spatial position에서의 filter를 통한 연산은 filter의 크기와 같은 75-dimensional(vector) dot product + bias 형태로 하나의 scalar를 output으로 출력한다. 이때 output은 해당 position에서 input image가 얼마나 filter와 일치하는지를 나타낸다.
위와 같은 연산을 하면 1x28x28 크기의 activation map이라는 output을 뽑아낸다.

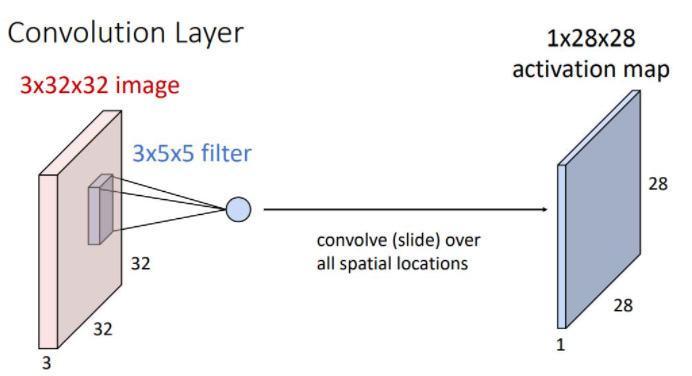
하나의 convolutional filter만 사용하는 것은 충분하지 않다. 그래서 아래 그림처럼 서로 다른 여러개의 filter을 사용해서 filter 수 만큼의 activation map을 만들어 낼 수 있다.

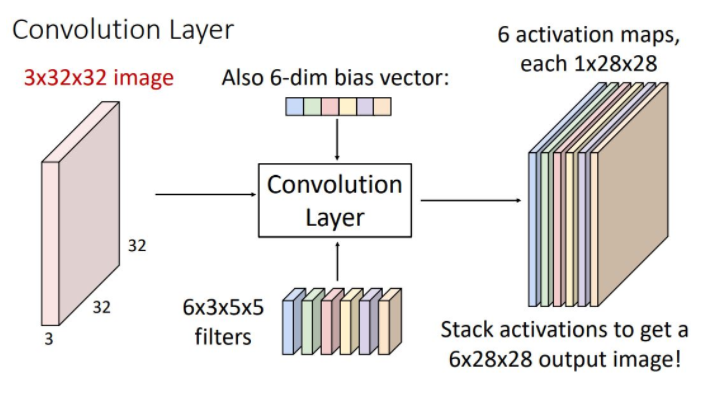
이러한 각각의 activation map은 input image의 각 spatial position이 얼마나 각각의 filter에 영향을 받았는가를 나타낸다. 이때의 activation map들을 concatenate시켜 하나의 3-dimesional tensor로 나타낼 수 있으며 그림의 예시는 6x28x28의 형태를 갖게 된다. 이러한 output을 또 다른 관점에서 본다면 각 point에서 6-dim vector를 가진 28x29 grid로 생각해 볼 수 있다.

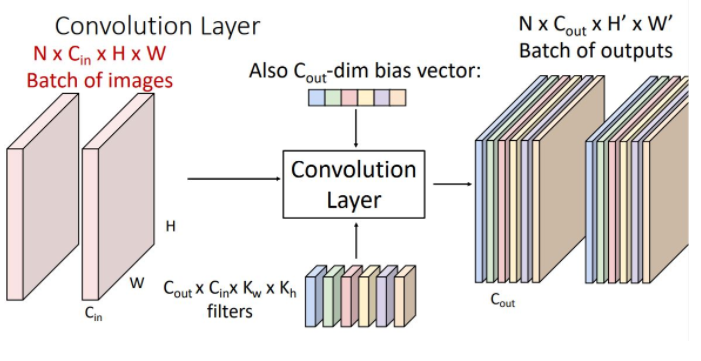
위와 같이 input을 batch로 사용할 수도 있다. 이때의 input image, filter, output는 4-dimensional tensor가 된다.

Stacking Convolutions

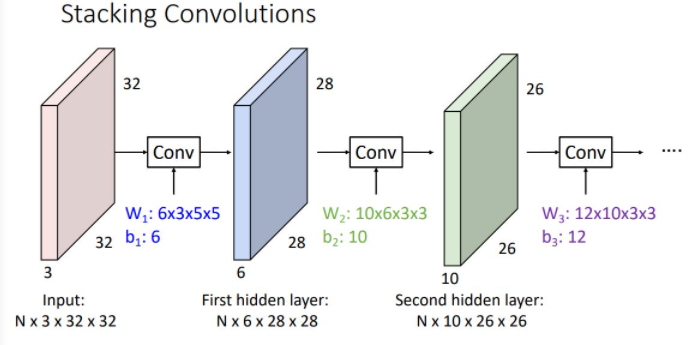
위 그림처럼 각 conv later에 있는 kernel(filter)의 수만큼 output이 나오게 되며 이는 다음 layer의 input으로 들어가게 되는 형태이다. 이때 각 layer의 input과 output이 되는 activation map들은 fully-connected network에서와 같이 hidden layer라고 말한다.

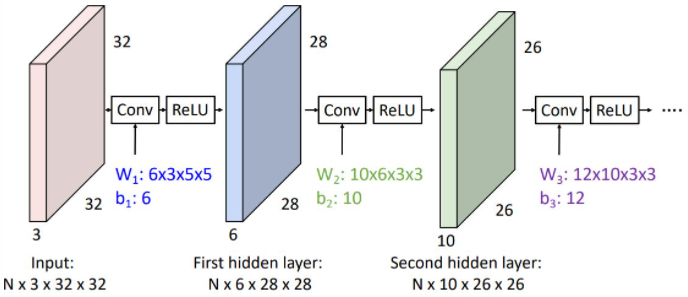
하지만 이런 형태의 convolution network에서는 각각의 convolution operator가 fully-connected network에서의 각 layer와 같이 linear operator에 지나지 않는다. 그렇기에 우리는 아래의 그림처럼 conv operator 직후에 (non-linear인) activation function을 취해준다.

Visual Viewpoint

1. Linear Classifier
   
   Linear Classifier는 클래스별로 하나의 weight vector만 가지고 있기에 클래스별 하나의 template만 가진 형태로 볼 수 있다.

2. Fully-Connected Neural Networks
   
   Fully connected neural network의 첫번째 layer를 살펴 보면 우리가 설정한 first hidden layer크기에 대응항하는 W1의 크기만큼 여러개의 template을 갖는 (Bank of whole-image templates을 갖는) 형태였다.

3. Convolutional Network
   
   

Convolutional Layer는 앞선 위의 2경우와는 달리 input image와 같은 크기의 template을 학습하는 것이 아닌 작고 local한 size의 template을 학습한다. 위의 그림은 AlexNet의 11x11 RGB image를 학습한 첫번째 layer의 filter이다. 이 각각의 filter들은 oriented edge정보와 opposing color 정보 등 low-level feature을 학습한 것으로 볼 수 있다.
이러한 각각의 filter들은 oriented edge, opposing color로 해석되는 정보를 통해 input image의 각 position이 얼마나 다음 hidden layer에 영향을 미치는 정도를 나타낸다.
다른 표현으로는 64-dimensional feature vector가 있고 각각의 vector는 하나의 input position에서의 64개의 feature를 학습한 형태로 생각해볼 수 있다.

Spatial dimensions

input이 7x7이고, Filter가 3x3일때 output은 5x5가 된다. 이를 공식화하면 input(W)-Filter(K)+1이 output이라고 할 수 있다.
convolution layer의 문제점으로는 레이어를 지날 때마다 feature map, 즉 데이터의 크기가 줄어든다는 문제점이 있다.
그래서 feature map 가장자리에 임의의 픽셀을 추가하는 padding이라는 것을 해주는데, 주위 픽셀의 평균으로 추가하거나, 근처의 값을 복사하는 등 여러가지 방법이 있지만 대부분의 경우, 그냥 0을 추가하는 zero padding이라는 것을 사용한다.

Hyperparameter P에따라 정해지는데 P가 정해지면 Input크기와 Filter의 크기가 각각 W,K라고 할때 Output의 크기는 W-K+1+2P가 된다. 그리고 보통 P의 값은 input과 output의 크기가 같게되는 (K-1)/2로 정하며 이렇게 할 경우 ‘Same Padding’이라고 부른다.

Receptive Fields

Convolution layer가 무엇을 하는지 생각해 볼 수 있는 또 다른 방식이 Receptive field이다. 이는 output image의 각 spatial position이 input image에서 얼만큼의 region에 영향을 받는가를 뜻한다. 이를 1-conv layer관점에서 살펴보면 다음과 같다.

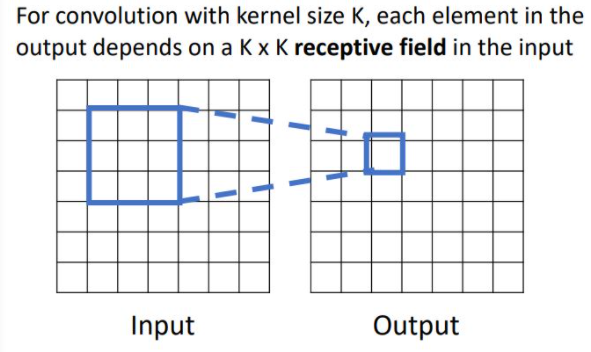
위의 그림에서는 3x3 region이 receptive field가 된다.

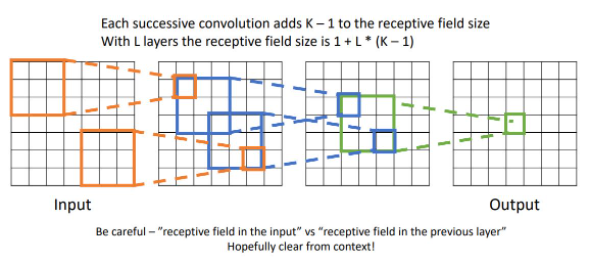
위 예시는 3-conv layer일때의 receptive field 예시이다. output tensor부터 점점 확장해 나가면 3x3 region이 5x5 region이 되고 7x7 region이 최종 receptive field size가 된다.
이러한 receptive field의 size를 1+L*(K-1)으로 계산할 수 있다. L은 Layer의 갯수이고 K는 kernel의 size(filter size)이다.
하지만 input image의 해상도가 커질수록(1024x1024) 그만큼 conv layer가 많아지며 (kernel size가 3일 경우 500개 가량의 convlayer가 필요) output에서 각 spatial position이 매우 큰 receptive field size를 커버한다는 뜻이므로 좋지 않은 형태이다. region이 3x3 -> 5x5 -> 7x7 -> 9x9 — -> 1024x1024 일케 확장 될 것. 다음과 같은 문제를 해결하기 위해 또 다른 hyper parameter를 적용하여 downsample 해주어야 한다.

Stride Convolution

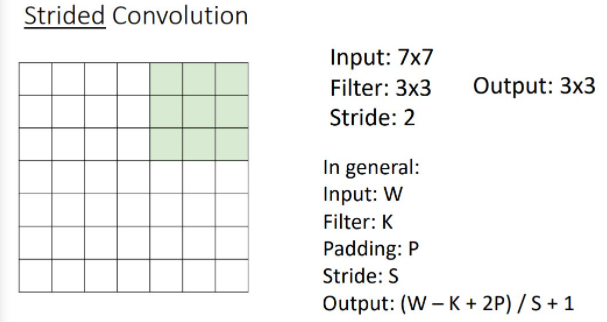
Stride는 필터가 Input위로 sliding할때, 얼마나 slide할 것인지, 정도를 나타내며, 보통 그 값을 S로 나타낸다. Stride 사용했을 시, Output의 크기는 ((W-K+2P)/S)+1이 되며 대부분의 경우 (W-K+2P)는 S로 나누어 떨어지며, 그렇지 않은 경우는 버림하거나 반올림을 한다고 한다.

Convolution Example

• Input volume : 3x32x32, 10 5x5 filters with stride 1, pad 2.
  
• output volume size:? -> 10x32x32
• Number of learnable parameter :
  parameters per filter : 355+1(for bias) = 76
  10filters, so total is 10*76=760
• Number of multiply-add operations :
  103232 = 10240 outputs; each output is the inner product of two 3x5x5 tensors(75 elems); total = 75*10240=768k
  

1x1 Convolution

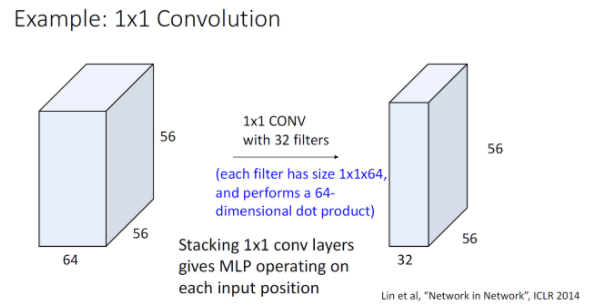
때때로 1x1크기의 필터를 사용하는 경우, 각 필터는 input의 feature vector마다의 linear layer로 볼 수 있는데 이렇게 되면 각각의 feature vector가 input의 원소로 존재하는 Fully-Connected Neural Network로 볼 수 있다. 추가적으로 Network in Network structure란 1x1conv -> relu -> 1x1conv -> relu 이런 형태의 network를 의미한다. 1x1 conv 이랑 fully-connected Neural Network는 같은 용도로 사용되지 않는다.

Common Setting

Other types of convolution

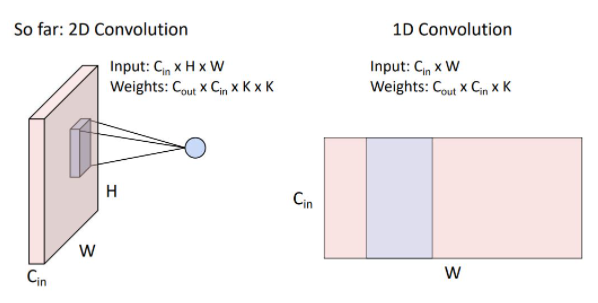
우리는 여지껏 2D convolution을 다뤘지만 가끔씩 실제로 1D convolution 형태를 볼 수 있다. 1D conv는 2-dimentional input을 갖고 weight matrix는 위 그림의 파란색 영역처럼 C_in x K size의 kernel C_out개를 갖는 형태이다. 1D conv는 일반적으로 sequence 형태의 textural data와 audio data에 많이 사용된다.

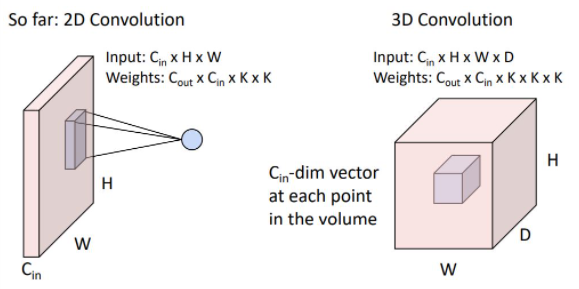
우리는 때때로 3D conv를 볼 수 있는데 이는 2D conv에서의 input이 batch형태로 이루어져있다고 생각할 수 있다. 이는 일반적으로 point cloud data 혹은 3d data에 사용된다.
우리가 지금가지 다뤘던 convolution layer들이 Pytorch에 Conv1d,2d,3d class로 구현되어 있다.

Pooling Layer

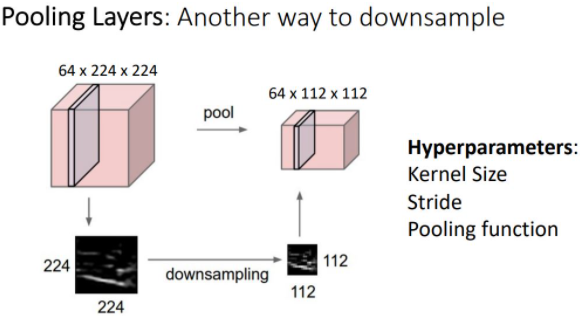
Pooling은 또다른 downsample 방식이다. 이전의 conv layer의 stride와 다른 점은 learnable parameter가 없다는 점이다. pooling layer에서는 hyperparameter로 kernel size와 stride,pooling function만 신경쓰면 된다.

• kernel size
• stride
• pooling
  

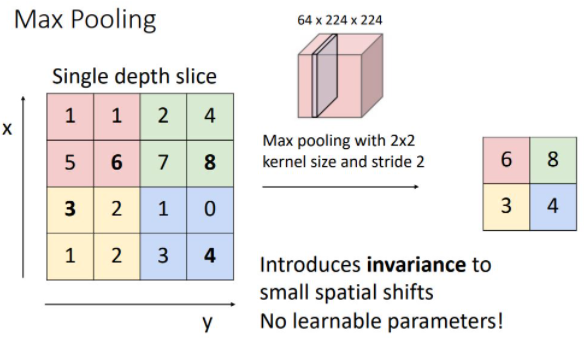
위 예시는 kernel size와 sride가 2인 2x2 max pooling을 하는 모습니다. kernel size와 stride가 2로 동일한 이유는 pooling region이 overlapping되지 않게 하기 위함이다. Alexnet에서는 K=3, S=2를 사용한다고 한다.

LeNet-5 (르넷5)

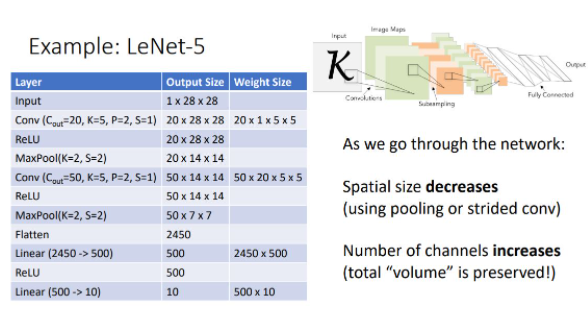
Convolutional Network의 classic architecture은 [Conv-Relu-Pool]의 반복이다.

• 질문 : Maxpooling이 nonlinearity 특성을 나타내는데 왜 Relu가 필요 ? -> 사실상은 별로 필요없음. 그냥 요즘 일반적으로 ReLU를 쓴다…
  

이러한 Classical architecture은 매우 커지고 매우 deep해져 매우 큰 data를 학습시키기 매우 힘들다는 문제가 있다. 이를 해결하기 위해 normalization 개념이 도입된다.

Batch Normalization

https://velog.io/@kangtae/EECS-498-007-598-005-72.-Normalization 여기 참고