Neural Networks

Feature Transfoms

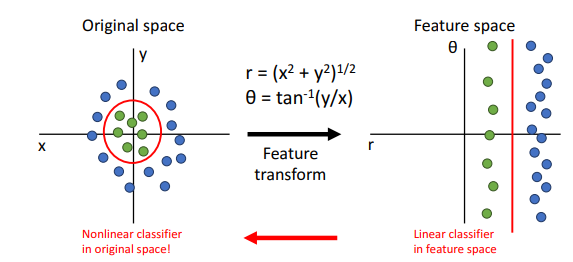
Linear Classifier는 간단한 만큼, Geometric Viewpoint나 Visual Viepoint에서 확인할 수 있듯이 한계가 있다. 이러한 한계는 Feature Transform으로 어느정도 극복이 가능하지만 현실적으로 고차원의 데이터를 적절히 Feature Transfomr하기 위해서는 고려해야 할 것이 많다. 그래도 Feature Transform을 잘 이용하기만 하면 괜찮은 성능을 보여주어 Computer Vision분야에서 많이 쓰인다.

Example of Feature Transforms

Color Histogram

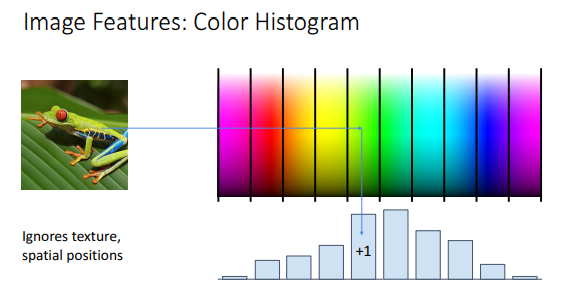
Color Histogram에서는 이미지의 구조 등은 무시하고 단순히 이미지에서 색상별 빈도를 가지고 히스토그램을 만들어서 이미지를 분석한다. 이 방식을 사용하면 기존의 이미지 속 객체의 각도나, 위치 등이 달라지는 문제 등에 대처할 수 있다.

Histogram of Oriented Gradients (HoG)

Histogram of Oriented Gradients(HoG)는 Color Histogram과 dual인 관계(?)이다. 이방식은 Color Histogram과는 달리 색상 정보는 다 빼고 local edege만 남기고 이것들만을 이용해서 이미지를 분석한다. HoG는 2000년대 중후반까지 Object Detection에서 많이 사용되었다.

Bag of Words (Data-Driven!)

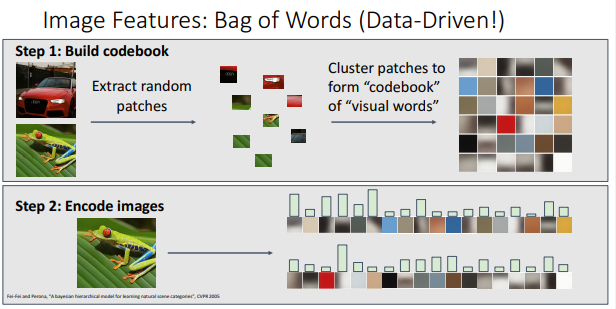
앞서 언급된 Color Histogram과, Histogram of Oriented Gradients 모두 어떤 feature를 어떻게 추출할 것이냐 등, 구현에 잇어서 많은 노력이 필요하였다. 그래서 구현에 있어 더 간단한 Bag of Words 라는 Data-Driven 방식이 새롭게 제안되었는데 이 방식은 2단계로 나뉜다. Step 1: 학스 데이터의 각 잉미지별로 무작위로 patch를 추출한 후에 각 patch들을 클러스터링해서 각 patch들의 군집으로 이루어진 ‘visual word’로 구성된 ‘codebook’를 만든다. Step 2 : 학습이 끝난 후 입력으로 이미지를 받으면 이미지에서 각 visual word가 얼마나 존재하는지, 히스토그램으로 표현한 후에 이미지를 분석한다.

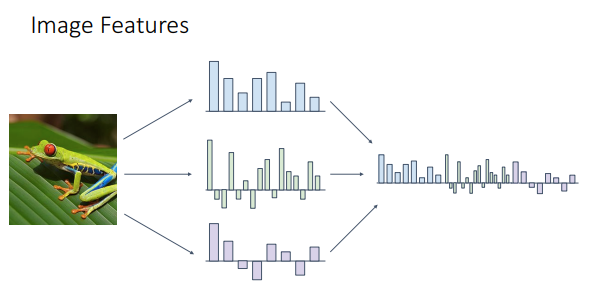
Feature Transfrom하는 방법은 하나로 딱 정하지 않아도 된다. 이미지에 대해서 Different Feature Representation 방법을 concatenate할 수 있다. 한마디로 앞에서 설명한 방법을 섞을 수 있다는 것이다. 이 방식은 2000년대 후반부터 2010년대 초반까지 widely하게 쓰였다.

2011 ImageNet Challenge의 우승자는 실제로 이 방식을 채택해서 우승했다. 이 때는 Alexnet이 나오기 바로 전이다.

Neural Networks

Neural Network, 즉 신경망 모델은 Linear Classifier를 적층해서 구성하며 대부분의 신경망 모델을 표현할 때, bias항은 관습적으로 생략한다.

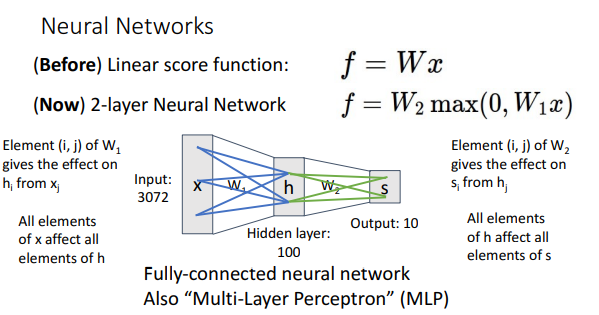
신경망 모델에서는 이전 레이어의 element가 다음 레이어의 element에 영향을 미치는 것을 알 수 있는데, 신경망 모델의 이러한 특성 때문에 Fully Connected Neural Network 혹은 Multi Layer Perceptron(MLP)로 부르기도 한다.

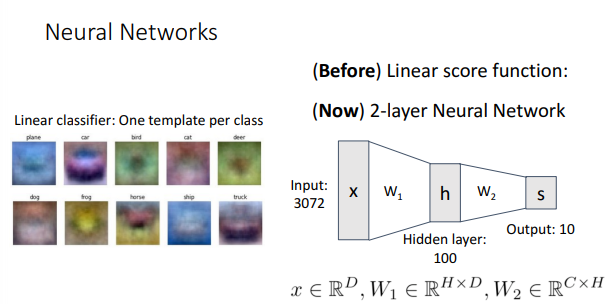
기존의 Linear Classifier는 각 카테고리당 1개의 템플릿만 만든다.

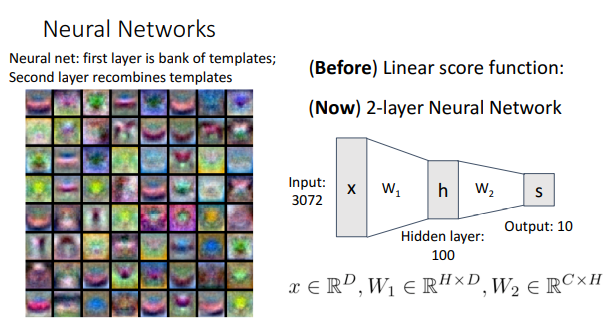
2-Layer Neural Network에서는 카테고리당 1개의 템플릿만을 만드는 것이 아니고, 첫 번째 레이어에서 각각의 Weight마다 템플릿을 만들어 내고, 두번째 레이어에서는 이전에 만든 템플릿을 재조합해서 class score를 만들어낸다. 이처럼 1개의 템플릿이 아닌 여러개의 템플릿의 조합으로 class를 표현한다고 해서 이 방식을 ‘Distributed Representation’이라고 부르기도 한다.

신경망 모델에서는 여러 개의 템플릿을 만들기에 중복된 정보를 가진 템플릿을 만들 수 있지만, Network Pruning과 같은 기술들로 어느정도는 해소할 수 있다.

Deep Neural Network

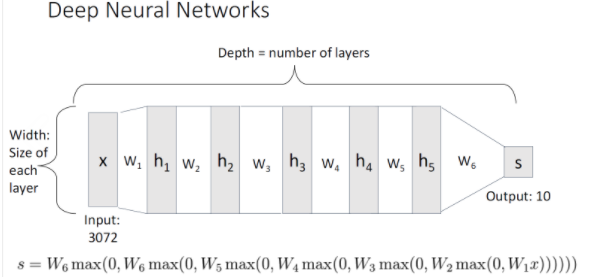
Neural Network에서의 layer의 수는 weight matrix의 수와 같다고 몰 수 있다. Depth는 layer의 수를 뜻하며 Width는 각 layer의 크기를 말한다.

Activation Function

\(f = W_2max(0,W_1x)\) 에서 max()함수가 나타내는 것은 Relu라고 Rectified Linear Unit이다. max함수 안의 input vector가 음수이면 0을 반환한다.

• What happens if we build a neural network with no activation function? \(s = W_2W_1x\)

신경망 모델에서 activation function을 적용하지 않으면 수학적으로는 Linear Classifier와 다를 바 없어지게 된다. (위의 그림 참고) activation function이 없는 신경망 모델을 deep neural network라고 부르는데 그래도 optimization 측면에서는 알아볼 가치가 있다고 한다.

relu말고도 다양한 activation function이 있는데 위의 sigmoid는 2000년대 중반까지 많이 쓰였으며 현재는 대부분 relu를 기본으로 하고 있는 추세이다. pretty good default choice임.

Space Warping

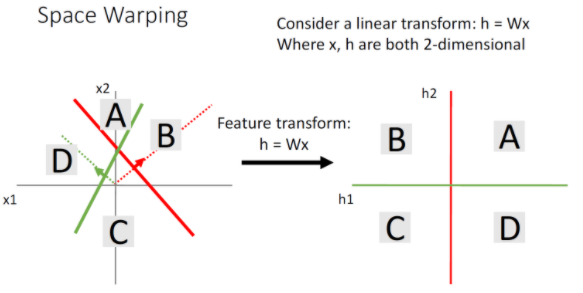
Neural Network가 Linear Classifier에 비해 우월한 성능을 나타내는 것은 Distributed Representation말고도 Space Warping 때문이다. Feature Tranform 방식은 Linear Transform이라서 데이터를 완전히 분리할 수가 없다.

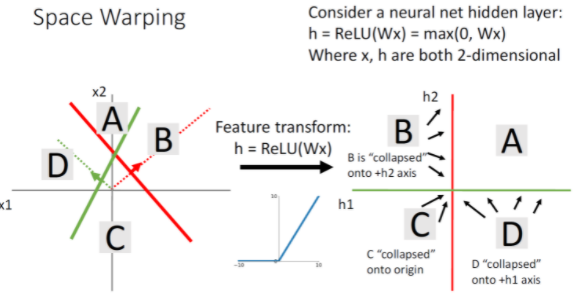
A영역의 경우 초록색 선으로부터 양수, 빨간색 선으로부터 양수이므로 1사분면에 위치하게 된다. B의 경우 Red feature로부터는 양수지만 green feature로부터는 negative이기에 2사분면에 위치하게 된다. 활성화 함수를 거치면 green feature에 대해 0이되게 된다. 그래서 B is collapsed onto h2 axis된다. C와 D또한 마찬가지고 음수가 나타날 때는 활성화 함수에 의해 0이되므로 축쪽으로 가까워지게 된다.

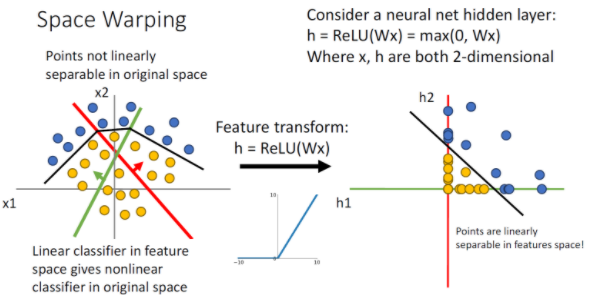
그러면 이렇게 데이터가 분리되어 Non linear하게 배치된 데이터도 적절하게 분리할 수 있게 된다.

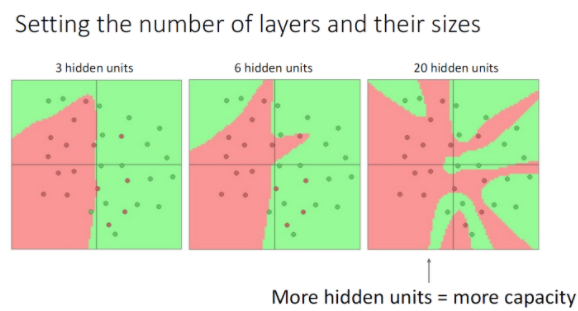
히든 레이어에서 더 많은 유닛을 사용하는 것은 데이터에 더 많은 line을 그어 구분하는 것과 동일한데, 그렇기 때문에 더 적은 유닛을 사용하면 과적합 문제를 완화할 수 있다.

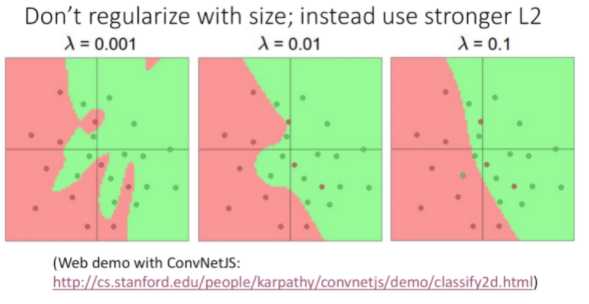
그렇다고 해서 유닛의 수로 이 문제를 처리하기 보다는 regularizer로 처리해야 한다.

Univeral Approximation

1개의 히든 레이어를 가진 신경망 모델로 어떤 함수든 근사하여 표현이 가능한데 이걸 Univeral Approximation이라고 한다.

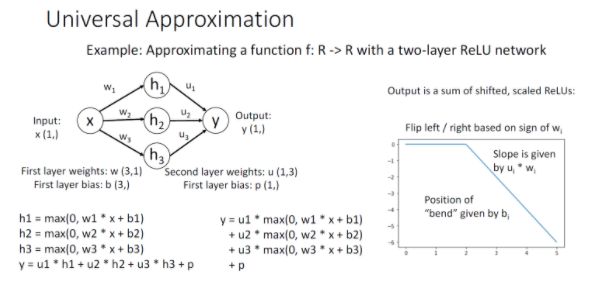
2-layer relu network의 출력 Y는 위와같이 나타난다. 이 Y는 shifted 되고 scaled ReLu function 의 합이라고 볼 수 있다.

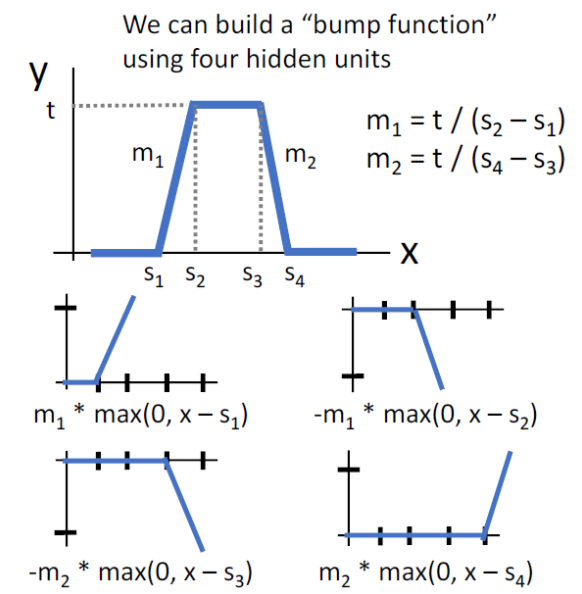
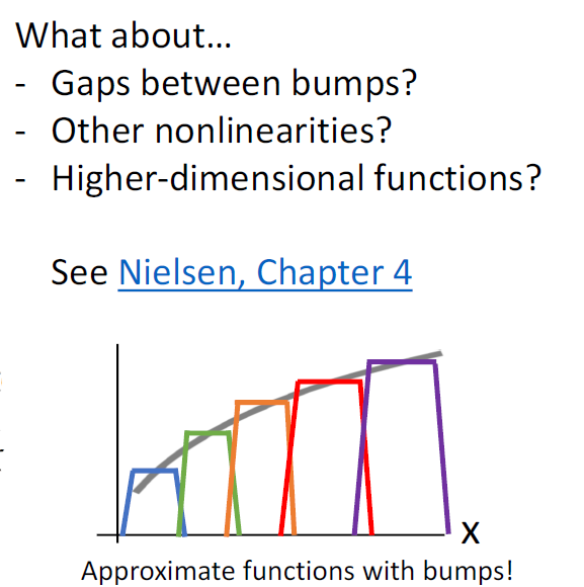
임의로 shift되고 scale된 4개의 relu를 모아서 위와 같은 bump function을 만들 수 있는데, 이 bump function을 이용하면 어떤 함수든 근사할 수 있으며, 그래서 2-layer neural network가 Univeral Approximation이 가능하다고 하는 것이다.

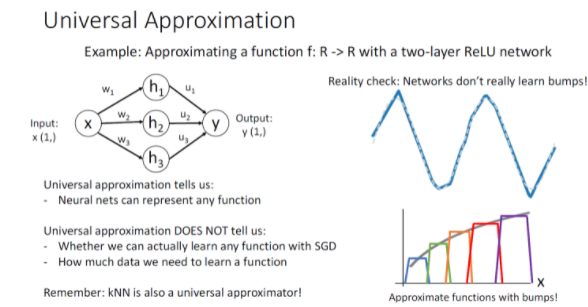
하지만 Neural Network로 Universal Approximation이 가능하다고 해서 Neural Network가 Bump Function 자체를 학습한다고는 볼 수 없다. 또한 Universal Apporximation은 Neural Network가 어떤 함수든지 표현이 가능하다는 사실만 알려줄 뿐, SGD를 사용했을 때도 어떤 함수든지 표현이 가능하다는 사실을 알려주는 것도 아니고 학습에 데이터가 얼마나 필요하다는 사실도 알려주지 않는다. 그래서 단순히 Universal Approximation이 가능하다고 해서 Neural Network가 최고의 모델이라는 주장은 옳지 않다. 낮은 성능을 보여주는 Knn도 Universal Approxiamtor이다!

Optimization

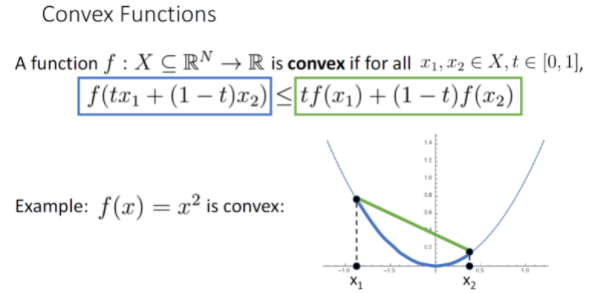
Convex vector란 두 점을 잇는 선분을 그었을 때, 항상 두 점 사이에 위치한 점들이 모두 선분 아래에 위치한다면 그 함수를 Convex Function이라고 한다. 왼쪽 식을 봤을 때 두 점 x1과 x2를 linear combination 한것을 f 함수에 집어넣었고 이 값이 오른쪽 식보다 작거나 같아야 한다는 것이다.

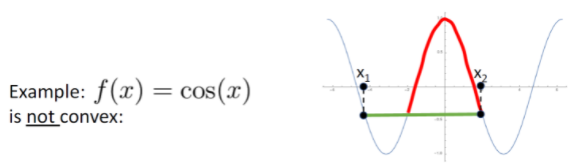
예를 들어 코사인 함수는 Convex function이 아니다.

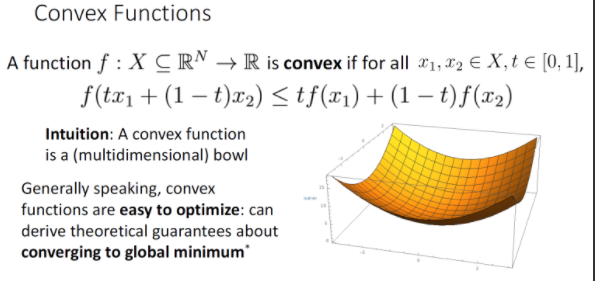
고차원 공간에서의 Convex Function은 bowl shape를 그리는 함수를 지칭하며 Convex Function은 기울기를 따라 내려간다면 간단히 global minimum에 도달할 수 있다. 그래서 Convex Function은 easy to optimize하다. 또한 초기화에 따른 영향도 덜하다.

Linear 모델은 convex optimization problem이다. 즉 linear model을 train할 때 항상 convex함수가 Global minimum에 도달할 것이 이론적으로 보장되어 있다. 그러나 Neural Network에서는 그러한 이론적 뒷받침이 존재하지 않아 그런 경우에는 Linear Model이 선호되기도 한다.

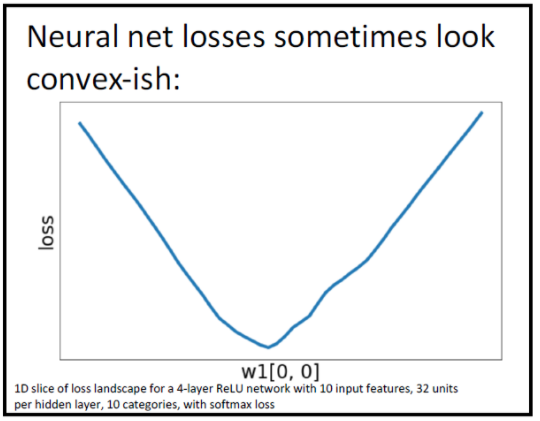
Neural Network에서는 Convex Function임을 확인하고 싶을 때, 고차원의 loss에서 Weight Vector W에서 1개 원소에 해당하는 slice를 떠서 확인하는데 slice가 Convex를 이룰 수도 있지만 아닐때도 있다. 아래 그림처럼

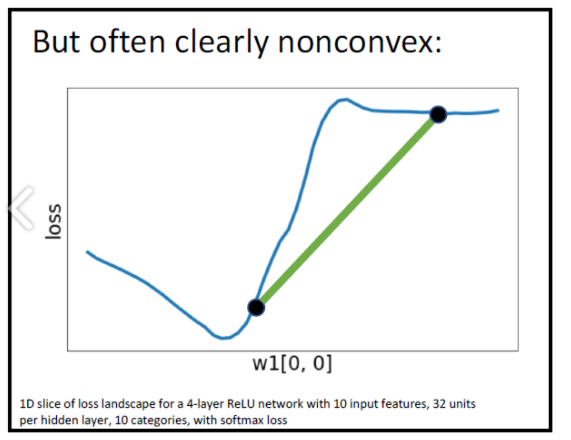
그래서 대부분의 Neural Network에서는 nonconvex를 이루는 데이터에 대해서도 optimization방안이 필요하다.