Abstract
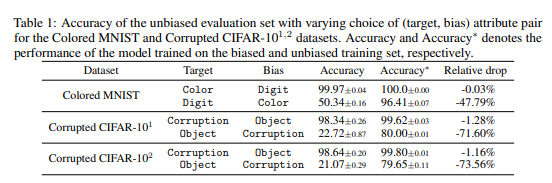
Self-supervised representation learning에서 주목받는 기술 중 하나는 의미론적으로 유사하고 다른 샘플 쌍을 대조하는 것입니다. 레이블에 접근할 수 없는 상태에서 다르다고 판단되는 (부정적인) 포인트들은 일반적으로 무작위로 샘플링된 데이터 포인트로 간주됩니다. 이는 암묵적으로 이러한 포인트들이 실제로는 동일한 레이블을 가질 수 있다는 점을 받아들이는 것입니다. 예상대로, 레이블이 실제로 다른 부정적 예제를 샘플링하면 성능이 향상되는 것을 합성 설정에서 관찰했습니다. 이러한 관찰에 자극받아, 우리는 진정한 레이블에 대한 지식 없이도 동일한 레이블 데이터 포인트의 샘플링을 수정하는 편향을 제거한 대조적 목적을 개발했습니다. 실증적으로, 제안된 목적은 시각, 언어, 강화 학습 벤치마크에서 최첨단 표현 학습을 지속적으로 능가합니다. 이론적으로는, 하류 분류 작업에 대한 일반화 경계를 설정했습니다.
Introduction
실제로, 기대값은 경험적 추정으로 대체됩니다. 각 훈련 데이터 포인트 x에 대해, 일반적으로 하나의 긍정적 예시를 사용합니다. 예를 들어, 그 예시는 변형으로부터 유도될 수 있고, N개의 부정적 예시 x가 사용됩니다. 실제 레이블이나 실제 의미론적 유사성이 일반적으로 사용할 수 없기 때문에, 부정적 대응물은 일반적으로 훈련 데이터에서 균일하게 추출됩니다. 그러나 이것은 negative pair가 실제로 x와 유사할 가능성이 있다는 것을 의미합니다, 이는 그림 1에서 설명되어 있습니다. 이 현상을 샘플링 편향이라고 부르며, 이는 경험적으로 중요한 성능 저하를 초래할 수 있습니다.


그러나 이상적인 편향되지 않은 목표는 실제로는 레이블을 알아야 하므로, 즉 지도 학습이 필요하므로 달성할 수 없습니다. 이 딜레마는 지도 없이 이상적인 목표와 표준 대조적 학습 사이의 격차를 줄일 수 있는지 여부를 제기합니다. 본 연구에서는 레이블이 없는 훈련 데이터와 긍정적인 예시에만 접근할 수 있다고 가정하면서도 이것이 실제로 가능하다는 것을 보여줍니다. 특히, 샘플링 편향을 수정하기 위해 새로운 수정된 손실을 개발하는데, 이를 편향 제거 대조적 손실이라고 부릅니다. 저희의 접근법이 근거하는 핵심 아이디어는 부정적인 예시의 분포를 간접적으로 근사하는 것입니다. 새로운 목표는 표준 대조적 손실을 최적화하는 어떠한 알고리즘과도 쉽게 호환됩니다. 실증적으로, 저희의 접근법은 시각, 언어, 그리고 강화 학습 벤치마크에서 현존하는 최첨단 기술을 능가합니다.
Setup and Sampling Bias in Contrastive Learning
$p_x^-(x’)$, $p_x^+(x’)$ 각각은 $x’$가 $x$의 true negative/positive pair일 확률은 뜻함.
실제로 감독되지 않은 상태를 유지하기 위해, 우리의 방법과, 다른 대조 손실은 데이터 분포와 데이터 증강 또는 문맥 문장에 의해 모방된 “surrogate” 양성 분포에서만 샘플을 추출합니다.
Sampling Bias
직관적으로, 양수 및 음수 쌍이 원하는 잠재 클래스에 해당하는 경우 대조 손실은 다운스트림 분류 작업에 가장 유익한 표현을 제공합니다. 따라서 최적화를 위한 이상적인 손실은 수식(2)와 같이 편향되지 않은 손실입니다.
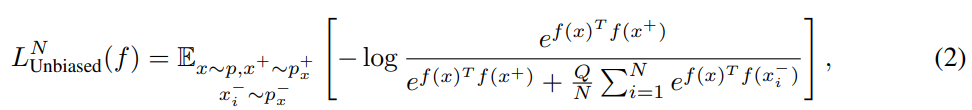
여기서 N은 negative pari의 갯수를, Q는 weight를 의미합니다. 일반적인 환경에선 Q=N으로 설정됩니다. 우리는 $p_x^-$에서 true negative를 sampling 해서 false negative bias를 피하고 싶습니다. 문제는 $p_x^-$에 대한 정보가 없기 때문에 $p_x^-$ 대신 $p$에서 (possible false) negative pair를 샘플링 합니다.
이 과정에서 false negative가 sampling되고, loss에 bias가 생기게 됩니다. 그래서 unbiased loss의 upper bound는 수식 (3)과 같습니다.
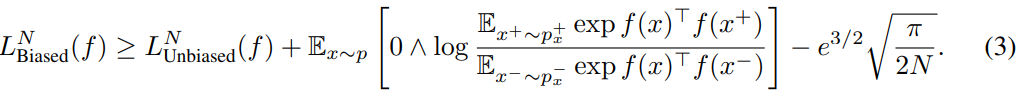
MoCo 등의 최근 방법들은 N=65536 등의 큰 숫자르 사용하기 때문에 마지막 항은 negligible 하다고 할 수 있고, Biased loss가 upper bound를 정의하므로 biased loss를 최소화 함으로써 unbiased loss도 최소화 할 수 있습니다.
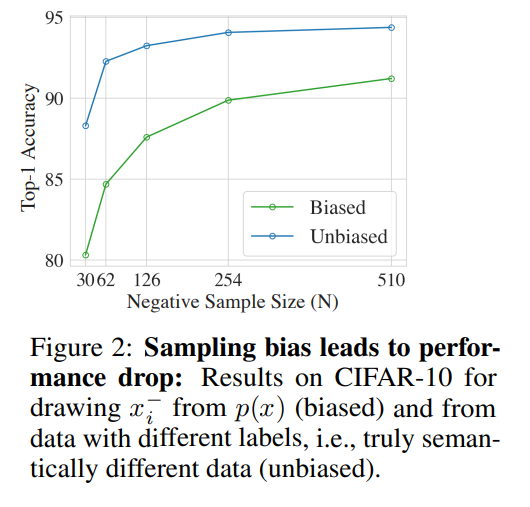
여기에 2가지 문제가 존재하는데, (1) unbiased loss가 작을 수록 두번째 항이 커져서 격차가 커진다 (2) 그림 2와 섹션 5의 실증적 결과는 상한값 $L_Biased^N$를 최소화하는 것과 이상적인 손실 $L_Unbiased^N$을 최소화하는 것이 매우 다른 학습된 표현을 결과로 가져올 수 있다는 것을 보여줍니다.
Dibiased Contrastive Loss
그림 2를 보면 실제로 Cifar-10을 가지고 학습을 하였을 때, top-1 accuracy에 대해서 unbiased/biased loss에 대한 결과가 차이나는 것을 보아 empirical하게 두 loss간에는 큰 차이가 난다는 것을 알 수 있습니다.
따라서 위의 부등식은 딱히 reliable한 관계를 주지는 못합니다.
이 논문에서는 class probability에 대한 prior를 통해 더 낮은 bias를 가지는 loss estimator를 찾습니다.
조금 더 자세히 말하면, negative pair 중 positive pair의 갯수가 몇 개인지에 따른 risk를 class probability prior를 통해 근사하는 것입니다.

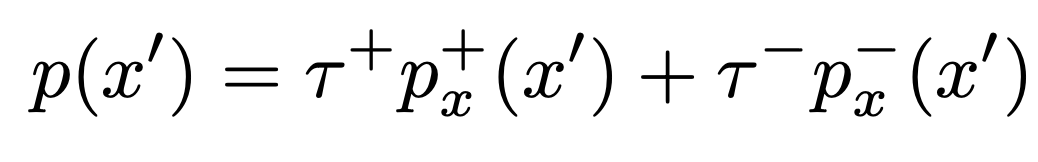
먼저, data distribution을 위와같이 decompose합시다. (둘의 support는 disjoint하다고 가정하는 것 같습니다)
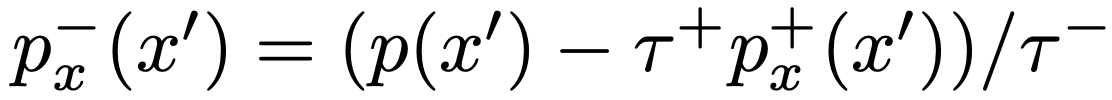
위와 같은 decomposition 하에서 $p_x^-$는 $p_x^+$를 통해 얻어 낼 수 있습니다. 위의 관계를 이용하여, expectation에 있는 $p_x^-$를 alternative form으로 쓰면 $p$, $p_x^+$에 대한 접근만으로 통해 $p_x^-$에서의 sampling을 근사할 수 있을 수도 있습니다.
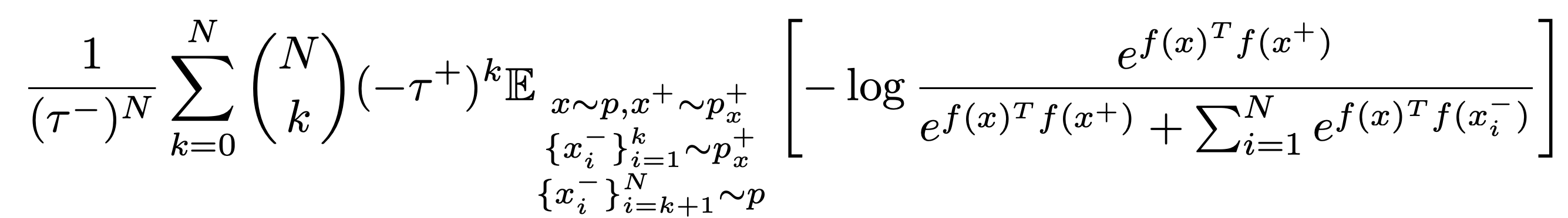
위의 식은 모든 combination에 대해 expectation의 estimate을 요구하기 때문에 computation cost가 크고, 최소 N개의 positive sample이 존재해야만 exact한 estimate가 됩니다. 따라서 위의 식을 direct하게 최소화 하는 대신 negative example (true negative + false positive)의 수 N이 커짐에 따라 unbiased estimator가 asymptotic하게 근사하는 분포를 찾습니다.
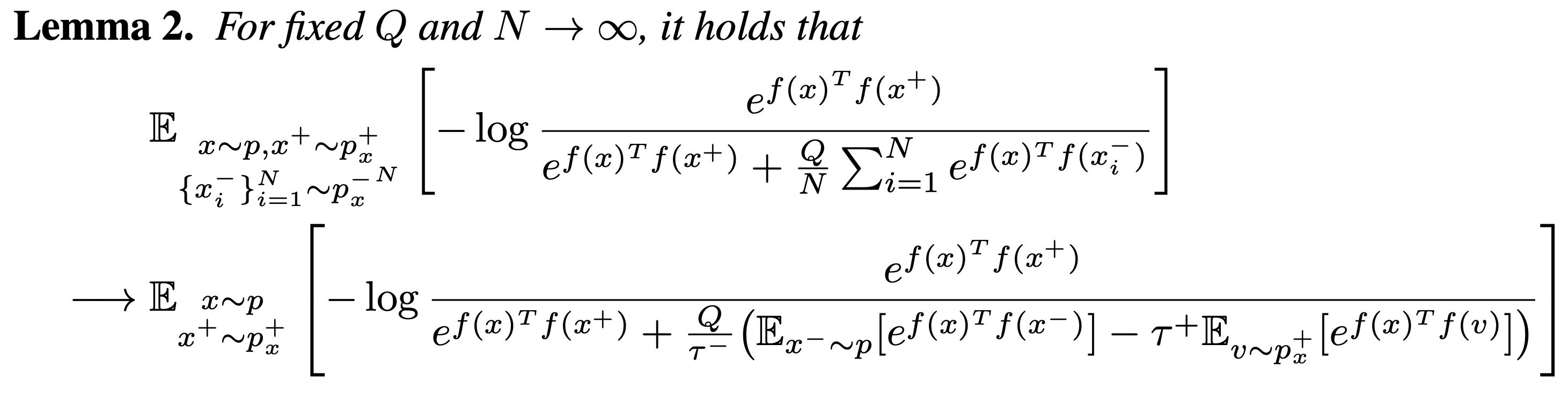
이 식은 여전히 $x^-$에서 $p$를 샘플링하지만, additional positive sample v를 추가하여 둘의 weight를 조정합니다.
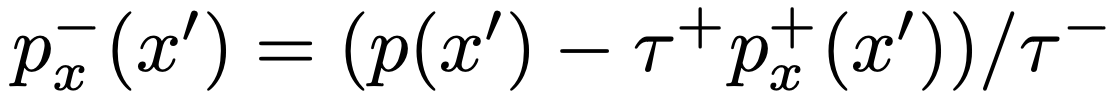
이는 또한 위에서 본 $p_x^-$의 indirect한 expression을 사용한 것으로, $p_x^+$와 $p$에 대한 expectation이 큰 expectation의 안으로 들어가면서 각각의 estimate가 decoupled되었다는 장점이 있습니다.
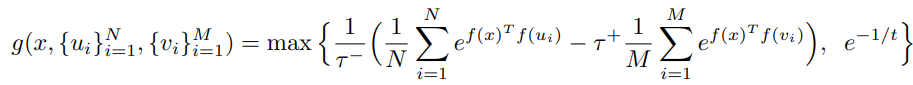
실제로 asymptotic distribution의 분모에 있는 두 번째 항을 empirical하게 계산하는 과정에서는 위의 식을 사용합니다.
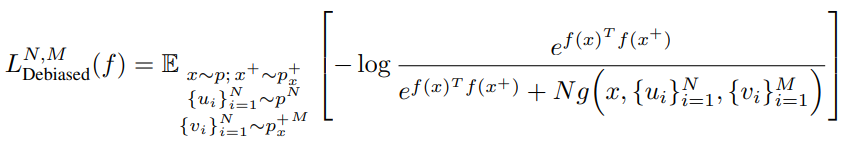
Q=N으로 두면 epirical loss는 위와 같이 정의됩니다.
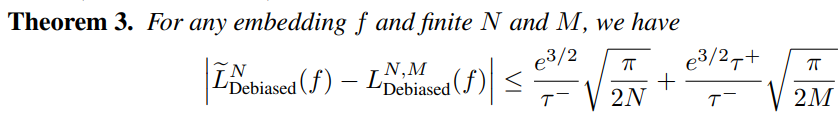
Asymptotic loss의 empirical loss에 대한 error bound는 위와 같습니다.
N과 M이 늘어나면 emprical expectation의 정확도도 올라가고, 따라서 오차가 줄어든다고 볼 수 있습니다.
Experiments
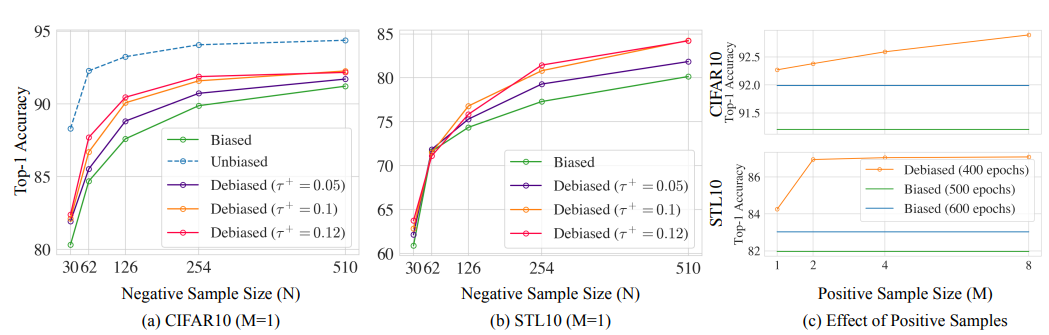
실제로 N-batch와 M-positive pair에 대한 ablation study 결과를 보았을 때 N과 M의 증가에 따라서 성능 증가가 따라오는 것을 볼 수 있습니다.
위에서 살펴본 것은 이 empirical loss가 asymptotic loss를 근사한다는 것, 그리고 N과 M의 증가에 따라 성능이 증가한다는 것 뿐이었습니다.
Empirical하게 negative bias가 줄어든 결과라고 말할 순 있겠지만, 실제로 그런지 이론적 분석 또한 뒷받침 되어야 할 것입니다.
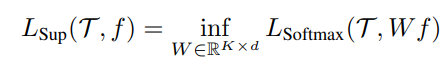
먼저, 이 논문에서는 encoder의 특정 classification task에 대한 성능을 encoder를 freeze했을 때 linear classifier를 통해 얻을 수 있는 성능의 최댓값으로써 정의합니다.
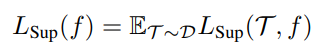
또한 encoder의 자체 성능을 일반적인 classification task에 대한 성능의 기댓값으로써 정의합니다.
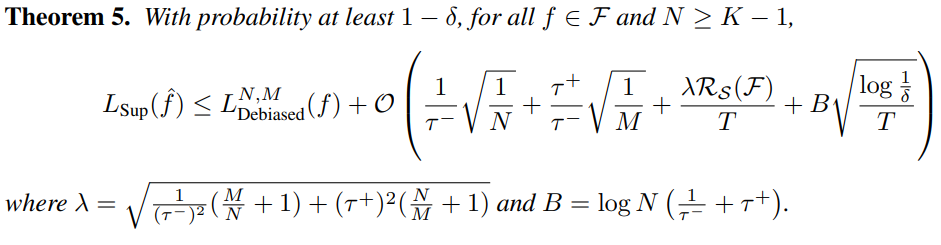
이 때 optimal backbone에 대한 upper bound는 다음과 같습니다.
우리가 주장하였듯 데이터셋의 크기 T, example의 수 N, positive pair의 수 M등이 커질수록 optimal loss에 대한 bound가 작아집니다.